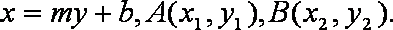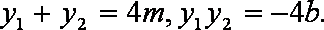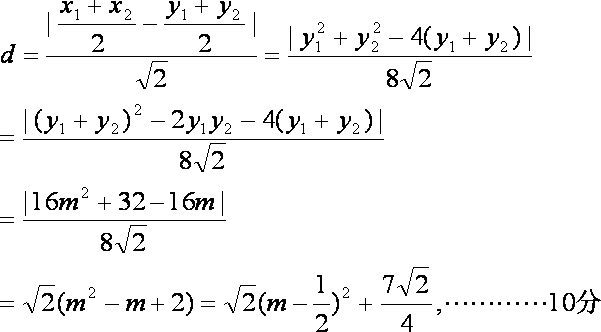抛物线的定义及应用
共118题

· 抛物线的定义及应用

抛物线的定义及应用
共118题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

已知抛物线上一点(m>0)到其焦点F的距离为5，该抛物线的顶点在直线MF上的射影为点P，则点P的坐标为　　　　　。

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 20 分

设点是抛物线的焦点，、、…、是抛物线上的个不同的点（，）。

（1）若抛物线上三点、、的横坐标之和等于4，求的值；

（2）当时，若，求证：；

（3）若将题设中的抛物线方程推广为，请类比小题（2），写出一个更一般化的命题及其逆命题，并判断其逆命题的真假. 若是真命题，请予以证明；若是假命题，请说明理由。

正确答案

见解析

解析

（1）解：抛物线焦点，准线方程为：.由抛物线定义得

，，，

∴ .

（2）证明：由，，，…，，

，

即.

则

（3）经推广的命题：

“当时，若，则.”

其逆命题为：

“当时，若，则”。

该逆命题为假命题。

不妨构造特殊化的一个反例：

设，，抛物线，焦点.由题意知：

；

根据抛物线的定义得：

；

不妨取四点坐标分别为、、、，但

，

所以逆命题是假命题。

知识点

抛物线的定义及应用

题型：简答题

简答题 · 18 分

设抛物线的焦点为，过且垂直于轴的直线与抛物线交于两点，已知.

（1）求抛物线的方程；

（2）过点作方向向量为的直线与曲线相交于两点，求的面积并求其值域；

（3）设，过点作直线与曲线相交于两点，问是否存在实数使为钝角？若存在，请求出的取值范围；若不存在，请说明理由。

正确答案

见解析

解析

（1）由条件得，抛物线C的方程为；

……………………………. 4分

（2）直线方程为代入，，

……………………………. 6分

恒成立。设，则，

……………………………. 7分

，……………………. 9分

。……………………………. 10分

（3）设所作直线的方向向量为，则直线方程为代入

得，设，.

……………………………. 12分

又，则，为钝角，，……………………………. 14分

即，

，该不等式对任意实数恒成立，……………….16分

因此.

……………………………. 17分

又，因此，当时满足条件。

……………………………. 18分

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

已知A、B是抛物线上的两点，O是抛物线的顶点，OA⊥OB。

（1）求证：直线AB过定点M（4，0）；

（2）设弦AB的中点为P，求点P到直线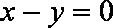的距离的最小值。

正确答案

见解析。

解析

（1）设直线AB方程为

将直线AB方程代入抛物线方程

………………2分则

（2）的距离

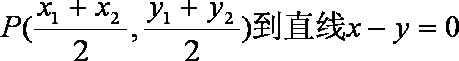
当 ………………14分

知识点

抛物线的定义及应用

题型：简答题

简答题 · 14 分

抛物线:上一点到抛物线的焦点的距离为3，为抛物线的四个不同的点，其中、关于y轴对称，，，，，直线平行于抛物线的以为切点的切线。

（1）求的值；

（2）证明：；

（3）到直线、的距离分别为、，且，的面积为48，求直线的方程。

正确答案

见解析

解析

（1）|QF|=3=2+， =2.

（2）抛物线方程为，

A()， D()， B() ，C()，

，，

，，，

，

所以直线AC和直线AB的倾斜角互补，。

（3）设，

则m=n=|AD|sin，，

即，

把与抛物线方程联立得：，

，，同理可得，

，

，。

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 抛物线的标准方程和几何性质

百度题库 > 高考 > 文科数学 > 抛物线的定义及应用

扫码查看完整答案与解析