抛物线的定义及应用
共118题

· 抛物线的定义及应用

抛物线的定义及应用
共118题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知焦点在轴上的椭圆的离心率为，它的长轴长等于圆的半径，则椭圆的标准方程是

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

已知为抛物线的焦点，抛物线上点满足。

（1）求抛物线的方程；

（2）点的坐标为(,)，过点F作斜率为的直线与抛物线交于、两点，、两点的横坐标均不为，连结、并延长交抛物线于、两点，设直线的斜率为,问是否为定值，若是求出该定值，若不是说明理由。

正确答案

见解析。

解析

（1）由题根据抛物线定义，

所以，所以为所求， ……………………………2分

（2）设,,,

则，同理………………4分

设AC所在直线方程为，

联立得所以， ………………………6分

同理(8分)

所以 …………………………………………9分

设AB所在直线方程为联立

得 ………………………………………………10分

所以

所以 ……………………………………………………………12分

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

已知抛物线的焦点为，直线与此抛物线相交于两点，则

正确答案

解析

设，，由题意可知，，，则，联立直线与抛物线方程消去得，，可知，故. 故选A.

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

已知抛物线C：焦点为F，点P是C上一点，若△POF的面积为2，则

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 13 分

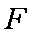
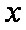
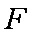
已知抛物线的顶点在原点，焦点在轴上，且抛物线上横坐标为1的点到的距离为2 ，过点F的直线交抛物线于A，B两点。

（1）求抛物线的方程；

（2）若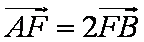，求直线AB的斜率；

（3）设点M在线段AB上运动，原点O关于点M的对称点为C，求四边形OACB面积的最小值。

正确答案

见解析

解析

（1）设抛物线方程为C：，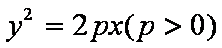

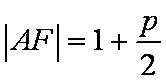
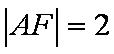
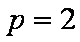
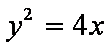
由其定义知，又，所以，.

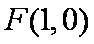
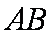
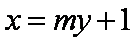
（2）依题意，设直线的方程为.

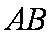
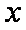
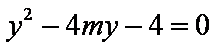
将直线的方程与抛物线的方程联立，消去得.

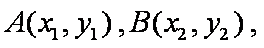
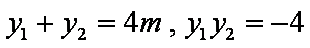
设所以 ………………①

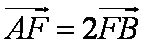
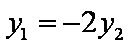
因为，所以 ………………②

联立①、②，消去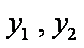得.

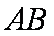
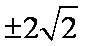
所以直线的斜率是.

（3）由点与原点关于点对称，得是线段的中点，

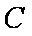
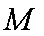
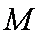
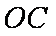
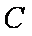
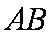
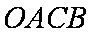
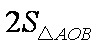
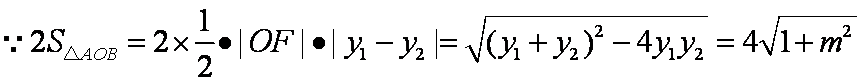
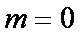
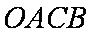
从而点与点到直线的距离相等，所以四边形的面积等于，

所以时，四边形的面积最小，最小值是.

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 抛物线的标准方程和几何性质

百度题库 > 高考 > 文科数学 > 抛物线的定义及应用

扫码查看完整答案与解析