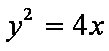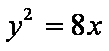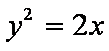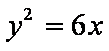- 抛物线的定义及应用
- 共118题
已知抛物线的顶点在坐标原点,焦点在

(1)求抛物线的标准方程;
(2)是否存在直线




若存在,求出直线的方程,若不存在,说明理由.
正确答案
见解析
解析
解:(1) 设抛物线方程为
由已知得:
所以抛物线的标准方程为
(2)不存在
因为直线与圆相切, 所以
把直线方程代入抛物线方程并整理得:
由

设












知识点
过抛物线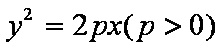
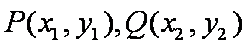
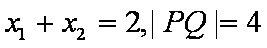
正确答案
解析
由抛物线的定义知: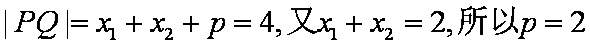
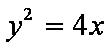
知识点
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,若|AF|=3.则|BF|=____ 。
正确答案
解析
易知直线的斜率不存在时,不满足题意;
当直线的斜率存在时,设过抛物线y2=4x的焦点F的直线为






知识点
如图,已知抛物线

(1)求抛物线
(2)过抛物线











正确答案
见解析
解析
(1)

所以

故


(2)任取点


由

由

记


因为

所以
所以
知识点
抛物线:







(1) 求抛物线



(2)设点


存在直线



若存在,求直线
正确答案
见解析
解析
解:
(1)抛物线

椭圆

则
(2)设直线




由

故

由





再由


故



由



于是点

由

从而
同理,
若



即

此方程无实根,所以不存在直线



知识点
扫码查看完整答案与解析