- 动能定理的应用
- 共327题
14.如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回。已知R=0.4 m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计。取g=10m/s2.
求:
(1)物块第一次经过圆轨道最高点B时对轨道的压力;
(2)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
正确答案
(1)、
(2)、L=1m
解析
解:(1)对物块,首次从A到B,有
在B点,有:
解得:
根据牛顿第三定律,小球对轨道的压力大小为40N,方向竖直向上。
(2)对物块,从A点到第二次到达B点:
在B点,有:
解得:L=1m
考查方向
解题思路
由于是单个物体做多过程、曲线运动的问题,所以要用动能定理列方程求解
易错点
(2)问中不脱离轨道返回A点的理解:只要物体能返回最高的B就能回到A点,所以 从A点到第二次到达B点:
在B点,有:
知识点
19.相距L=1 m的足够长金属导轨竖直放置,质量为m1=1 kg的金属棒ab和质量为m2=0.02 kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上,如图所示,虚线上方磁场的磁感应强度B=1T,方向垂直纸

⑴当时间t=2s时拉力F的大小;
⑵当cd棒通过2C的电量时,其产生的热量为2.5J,则外力F需要做功为多少;
⑶判断cd棒将做怎样的运动,求出cd棒达到最大速度所需的时间t0,
正确答案
(1)F=11.5N
(2)WF=93J
(3)见解析
解析
⑴ 



⑵ 





⑶ cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;后做加速度逐渐增大的减速运动,最后停止运动.当cd棒速度达到最大时,有:


对abcd回路,有:

又
fcd随时间变化的图象如图所示。
考查方向
解题思路
(1)由E=BLv、 
(2)由



(3)分析cd棒的运动情况:cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;然后做加速度逐渐增大的减速运动,最后停止运动.
cd棒达到最大速度时重力与摩擦力平衡,而cd棒对导轨的压力等于安培力,可求出电路中的电流,再由E=BLv、欧姆定律求出最大速度.
易错点
本题中cd棒先受到滑动摩擦,后受到静摩擦,发生了突变,要仔细耐心分析这个动态变化过程.滑动摩擦力与安培力有关,呈现线性增大.
知识点
如图所示,绝缘轨道CDGH位于竖直平面内,圆弧段DG的圆心角为θ=37°,DG与水平段CD、倾斜段GH分别相切于D点和G点,CD段粗糙,DGH段光滑,在H处固定一垂直于轨道的绝缘挡板,整个轨道处于场强为E=1×104 N/C、水平向右的匀强电场中。一质量m=4×10-3
38.滑块在GH段上的加速度;
39.滑块与CD段之间的动摩擦因数µ;
40.滑块在CD段上运动的总路程。某同学认为:由于仅在CD段上有摩擦损耗,所以,滑块到达P点速度减为零后将不再运动,在CD段上运动的总路程为L+
正确答案
0
解析
GH段的倾角θ=37°,滑块受到的重力mg=0.04N,电场力qE=0.03N,qEcosθ=mgsinθ=0.024N,故加速度a=0
考查方向
解题思路
这道题首先根据受力分析求解加速度,利用动能定理列式求解摩擦力做功
易错点
摩擦力做功时要注意摩擦力往返都是做负功
正确答案
0.25
解析
滑块由C处释放,经挡板碰撞后第一次滑回P点的过程中,由动能定理得:
考查方向
解题思路
这道题首先根据受力分析求解加速度,利用动能定理列式求解摩擦力做功
易错点
摩擦力做功时要注意摩擦力往返都是做负功
正确答案
2.4m
解析
该同学观点错误,滑块在CD段上受到的滑动摩擦力Ff=µmg=0.01N,小于0.03N的电场力,故不可能停在CD段。滑块最终会在DGH间来回往复运动,到达D点的速度为0,全过程由动能定理得:qE·L+(-Ff·s)=0-0,解出s=
考查方向
解题思路
这道题首先根据受力分析求解加速度,利用动能定理列式求解摩擦力做功
易错点
摩擦力做功时要注意摩擦力往返都是做负功
15.如图所示,一个光滑绝缘细椭圆环固定放置在水平面上,其长轴AC的延长线两侧固定有两个等量异号点电荷,电量绝对值为Q,两者连线的中点O恰为椭圆的中心,BD为椭圆的短轴。一带电量为q的小球套在环上(q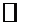
正确答案
解析
A选项,由于vC < vA,根据动能定理,可知从A到C动能减小,电势能增加,电场力做负功,小球带负电,故错误。
B选项,根据正负电荷周围电场强度的分布特点,可知电场强度,沿两电荷连线先减小后增大,连线的中点电场强度最小,故小球在A点受到的电场力大于在B点受到的电场力,故错误。
C选项,如图所示异号点电荷的等势面分布,可知B、D两点电势相等,小球从B点到D点电场力不做功,动能不变,故C选项正确。
D选项,小球从A到C过程中动能减小,电势能增加,从C到A动能增加,电势能减小,故C点电势能最大,故错误。
考查方向
1、考查正负电荷在真空中,电场、电势分布的对称性。
2、考查点电荷间的静电引力公式:
3、电场能与动能之间的相互转化,功能关系,动能定理,电场力做功。
解题思路
A选项,由于vC < vA,根据动能定理,可知从A到C动能减小,电势能增加,电场力做负功,小球带负电,故错误。
B选项,根据正负电荷周围电场强度的分布特点,可知电场强度,沿两电荷连线先减小后增大,连线的中点电场强度最小,故小球在A点受到的电场力大于在B点受到的电场力,故错误。
C选项,如图所示异号点电荷的等势面分布,可知B、D两点电势相等,小球从B点到D点电场力不做功,动能不变,故C选项正确。
D选项,小球从A到C过程中动能减小,电势能增加,从C到A动能增加,电势能减小,故C点电势能最大,故错误。
易错点
对正负电荷在真空中,电场、电势的对称性分布理解不到位。
知识点
如图所示,一倾斜传送带与水平方向夹角37°。传送物体。已知传送带总长度LAB =9.75m,以恒定速度v=2.0m/s顺时针转动。在距传送带底端A点9m的C点上方存在水平向左的匀强电场,电场强度50000N/C,现将一个质量m=2.0kg,电量
15.若不加电场,物块由底端A放上到相对传送带静止,物块相对传送带的位移S相;
16.加电场后,物块由底端A传送到顶端B所用时间t;
17.加电场后,将物块由底端A传送到顶端B过程中,传送带克服物块摩擦力做功W。
正确答案
5m;
解析
(1)对物体: μmgcosθ-mgsinθ=ma1 ----------1分
加速过程: V=a1t1 ----------1分
物块:S1=a1t12 /2 
传送带:S2=Vt1 ----------1分
相对位移:S相=S2-S1
解得a1=0.4m/s2 t1=5s S1=5m S2=10m S相=5m ----------1分
考查方向
解题思路
首先通过运动学特征分析物体的加速度,通过对物体受力分析求加速度,利用功能关系求克服摩擦力做功。
易错点
牛顿第二定律在求加速度时要注意将电场力计算进去
正确答案
7.5s;
解析
(2)加电场后:
匀速运动过程中:t2=(LAC-s1)/v ----------1分
CB段:mgsinθ+Eqcosθ-μ(mgcosθ-Eqsinθ)=ma2 ----------2分
减速过程中:sCB=vt3- a2t32/2 ----------1分
V’=v-a2t3 ----------1分
解得:t2=2s a2=2m/s2向下 t3=0.5s v’=1m/s
所以t总=t1+t2+t3=7.5s ----------2分
考查方向
解题思路
首先通过运动学特征分析物体的加速度,通过对物体受力分析求加速度,利用功能关系求克服摩擦力做功。
易错点
牛顿第二定律在求加速度时要注意将电场力计算进去
正确答案
187J
解析
(3)减速过程中物块相对传送带位移S’相=vt3-sCB 
A-C 摩擦生热Q1=μmgcosθS相 ----------1分
C-B 摩擦生热Q2=μmgcosθS’相 ----------1分
解得:S’相=0.25m, Q1=64J Q2=2.75J 总摩擦生热Q= Q1+ Q2
A— B功能关系得:
W-EqsCBcosθ=mgLABsinθ+mv2/2+Q ---------2分
得:W=187J
所以传送带克服物块摩擦力做功为187J。 ----------1分
考查方向
解题思路
首先通过运动学特征分析物体的加速度,通过对物体受力分析求加速度,利用功能关系求克服摩擦力做功。
易错点
牛顿第二定律在求加速度时要注意将电场力计算进去
扫码查看完整答案与解析