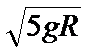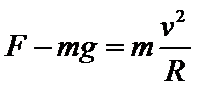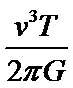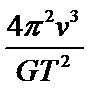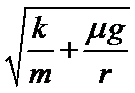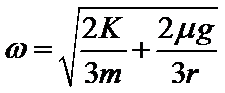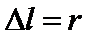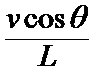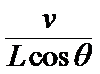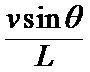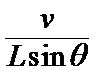- 曲线运动、万有引力
- 共1187题
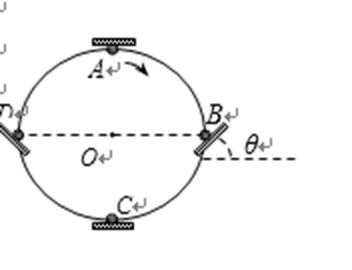
18.太极球是广大市民中较流行的一种健身器材。将太极球(拍和球)简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做半径为R的匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势。A为圆周的最高点,C为最低点,B、D与圆心O等高。球的质量为m,重力加速度为g,则
正确答案
解析
A、设球运动的线速率为v,半径为R,则在A处时: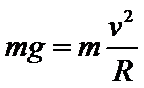
解得:F=2mg,即在C处板对球所需施加的力比A处大mg,故A错误;
B、球在运动过程中,动能不变,势能时刻变化,故机械能不守恒,故B错误;
C、球在任意时刻的速度大小相等,即球在最低点C的速度最小值为等于在最高点最小速度,根据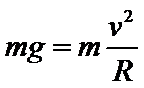
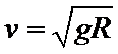
D、在B处合力提供向心力,即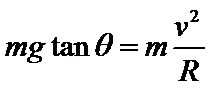
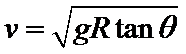
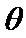
考查方向
解题思路
球在运动过程中受重力和支持力,由向心力公式可以求在各点的受力情况,并结合机械能守恒的条件分析即可。
易错点
抓住球在竖直面内始终不脱离板而做半径为R的匀速圆周运动,分析受力情况,注意合力提供小球运动的向心力。
知识点
15.如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图。M、N是两个共轴圆筒的横截面,外筒N的半径为R,内筒M的半径比R小得多,可忽略不计。筒的两端封闭,两筒之间抽成真空,两筒以相同角速度ω绕其中心轴线匀速转动。M筒开有与转轴平行的狭缝S,且不断沿半径方向向外射出速率分别为v1和v2的分子,分子到达N筒后被吸附,如果R、v1、v2保持不变,ω取某合适值,则以下结论中正确的是( )
正确答案
解析
若微粒运动时间为N筒转动周期的整数倍,微粒只能到达N筒上固定的位置,因此,故A错误;微粒从M到N运动时间t=





考查方向
解题思路
微粒从窄缝射出后沿筒的半径方向做匀速直线运动,同时N筒以角速度ω绕轴线转动,当微粒到达N筒时,二者运动时间相等,通过时间相等关系求解作出判断。
易错点
明确微粒运动的时间与N筒转动的时间相等,在此基础上分别以v1、v2射出时来讨论微粒落到N筒上的可能位置。
知识点
11.未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示。当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力,为达到目的,下列说法正确的是( )
正确答案
解析
为了使宇航员在航天器上受到与他站在地球表面时相同大小的支持力,即为使宇航员随旋转舱转动的向心加速度为定值,且有a=g,
宇航员随旋转舱转动的加速度为:a=ω2R,由此式可知,旋转舱的半径越大,转动的角速度就应越小,此加速度与宇航员的质量没有关系,所以选项ACD错误,B正确.
考查方向
解题思路
首先分析出该题要考察的知识点,就是对向心加速度的大小有影响的因素的分析,列出向心加速度的表达式,进行分析即可得知正确选项.
易错点
关键是从相关描述中提起有用的东西,对于该题,就是得知在向心加速度不变的情况下,影响向心加速度大小的物理量之间的变化关系,该题还要熟练的掌握有关匀速圆周运动的各个物理量的关系式,并会应用其进行正确的计算和分析.
知识点
6. 美国宇航局通过哈勃望远镜发现冥王星的“姐妹星” 鸟神星有一个小月亮,本次发现的鸟神星卫星具有重大意义,通过测量这颗小月亮的轨道,天文学家可以洞察它的演化,假设小月亮以速度v绕鸟神星做匀速圆周运动,测出运动的周期为T,已知引力常量为G,不计周围其他天体的影响,则下列说法正确的是( )
(在每小题给出的四个选项中,至少有一个选项是正确,全部选对的得6分,选对但不全的得3分,不选或有选错的得0分。)
正确答案
解析
A、C.根据圆周运动知识得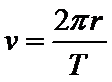
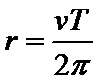
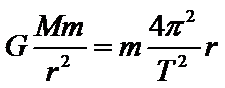
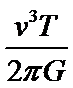
B.根据题意是小月亮围绕鸟神星做匀速圆周运动,根据万有引力定律仅题目已知条件无法求出小月亮的质量,故B错误;
D.根据向心加速度公式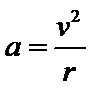
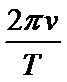
故本题选ACD
考查方向
解题思路
已知小月亮的线速度v与绕鸟神星的周期T,由圆周运动知识可得小月亮运动的轨道半径;根据万有引力提供向心力利用周期关系可解得鸟神星的质量,由圆周运动向心加速公式可解得小月亮的向心回速度值;
易错点
明确小月亮绕中心天体鸟神星做匀速圆周运动,因题目已知条件无法解得小月亮的质量。
知识点
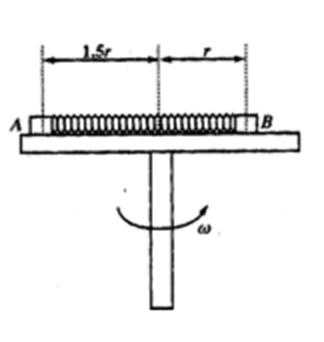
8. 如图所示,有一水平转台,上面放置着用轻质弹簧连接的小物体A、B使其随转台一起匀速转动,A、B的质量分别为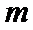
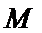
(在每小题给出的四个选项中,至少有一个选项是正确,全部选对的得6分,选对但不全的得3分,不选或有选错的得0分。)
正确答案
解析
因为A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,所以弹簧伸长量为
由于A、B随转台一起匀速转动,可知角速度相同.
A.当B受到的摩擦力为0时,弹簧弹力提供B的向心力,由牛顿第二定律得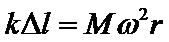
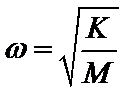
B. 当A受到的摩擦力为0时, 弹簧弹力提供A的向心力,由牛顿第二定律得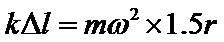
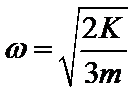
C. 当B刚好要滑动时,对B由摩擦力与弹簧弹力提供向心力,由牛顿第二定律得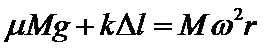
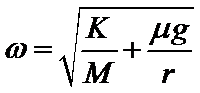
D. 当A刚好要滑动时对A由摩擦力与弹簧弹力提供向心力,由牛顿第二定律得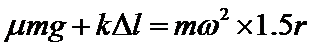
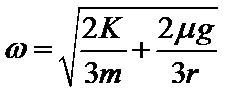
考查方向
解题思路
由题意先计算出弹簧的形变量,然后根据A与B的相应条件,找出向心力,依据牛顿第二定律分析求解。
易错点
根据A与B的相应条件,关键进行正确的受力分析,找出在各自相应条件下的向心力。
知识点
11.某原子电离后其核外只有一个电子,若该电子在核的静电力作用下绕核做匀速圆周运动,那么电子运动
正确答案
解析
根据原子核对电子的库仑力提供向心力,由牛顿第二定律得
对比以上选项,则答案为C
考查方向
解题思路
根据库仑定律求出原子核与核外电子的库仑力.
根据原子核对电子的库仑力提供向心力,由牛顿第二定律求出角速度,加速度,周期,线速度进行比较.
易错点
根据题意找出原子核与核外电子的库仑力提供向心力,并列出等式求解.
对于等效环形电流,以一个周期为研究过程求解.
知识点
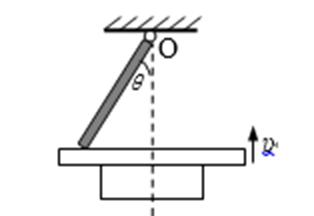
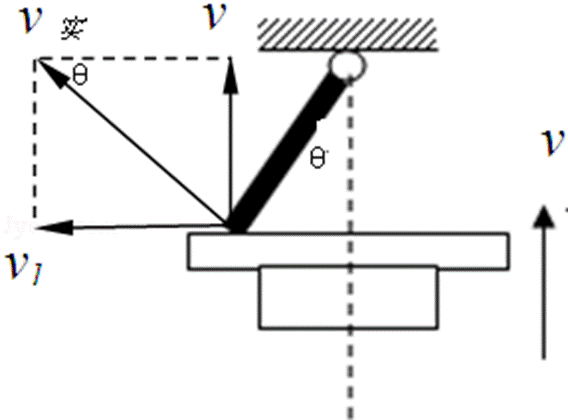
15.如图,长为L的直棒一端可绕固定轴O在竖直平面内转动,另一端搁在升降平台上,平台以速度υ匀速上升,当棒与竖直方向的夹角为θ时,棒的角速度为
正确答案
解析
棒与平台接触点的实际运动即合运动方向是垂直于棒指向左上,如图所示,
合速度v实=ωL,沿竖直向上方向上的速度分量等于v,即ωLsinθ=v,
所以ω=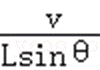
考查方向
解题思路
应清楚棒与平台接触点的实际运动即合运动方向是垂直于棒指向左上,竖直向上是它的一个分速度,把速度分解,根据三角形知识求解.
易错点
找合速度是本题的关键,应明白实际的速度为合速度.然后分解速度,做平行四边形,根据三角形求解
知识点
如图甲所示为测
27.请将下列实验步骤按先后排序:____________。
①使电火花计时器与圆形卡纸保持良好接触②接通电火花计时器的电源,使它工作起来③启动电动机,使圆形卡纸转动起来④关闭电火花计时器,关闭电动机;研究卡纸上留下的一段痕迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值
28.(单选题)要得到ω的测量值,还缺少一种必要的测量工具,它是
29.写出角速度ω的表达式ω=______,并指出表达式中各个物理量的意义:___________。
正确答案
①③②④……2分
解析
该实验先将电火花计时器与圆形卡纸保持良好接触,先使卡片转动,再打点,最后取出卡片进行数据处理.故次序为①③②④.
考查方向
解题思路
该实验应先安装器材,再启动电动机,然后接通电源打点,最后关闭电源,取出卡片,测量进行数据处理.
易错点
本题的关键知道该实验的实验原理ω=
正确答案
解析
要测出角速度,需要测量点跟点间的角度,需要的器材是量角器.故选:D.
考查方向
解题思路
打点计时器可以记录时间,要求角速度,还得知道在一定的时间里转过的角度,这点可用量角器测量.
易错点
本题的关键知道该实验的实验原理ω=
正确答案

解析
根据ω=

考查方向
解题思路
角速度ω=
易错点
本题的关键知道该实验的实验原理ω=
24.如图所示,一质量为m的小方块(可视为质点),系在一伸直的轻绳一端,绳的另一端固定在粗糙水平面上,绳长为r。给小方块一沿垂直轻绳的初速度v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为
正确答案
均匀
解析
利用“化曲为直”的思想,小方块在运动一周的过程中,可以看做小方块做加速度为a=μg的匀减速直线运动,则绳的拉力为:F=



考查方向
解题思路
1.小方块做圆周运动,则小方块受到绳子的拉力提供向心力;2.利用“化曲为直”的思想,小方块在运动一周过程中,可以看做小方块做加速度为a=μg的匀减速直线运动,则v2=2ax=2μgx,又因为x=rθ,所以F=
易错点
掌握“化曲为直”的思想,小方块在运动一周过程中,可以看做小方块做加速度为a=μg的匀减速直线运动
知识点
5.两根长度不同的细线下面分别悬挂两个小球,细线上端固定在同一点。若两个小球以相 同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个摆球在运动过程中,相 对位置关系示意图可能正确的是()
正确答案
解析
小球做匀速圆周运动,mgtanθ=mω2Lsinθ,整理得:Lcosθ=
考查方向
解题思路
小球做匀速圆周运动,靠拉力和重力的合力提供向心力,结合牛顿第二定律从而分析判断
易错点
本题的关键知道小球做匀速圆周运动向心力的来源,结合牛顿第二定律进行求解,另外本题关键要得出Lcosθ的关系式.
知识点
扫码查看完整答案与解析