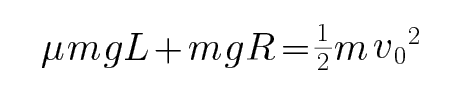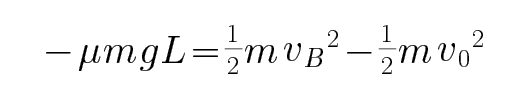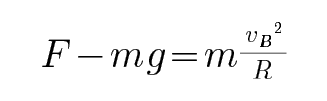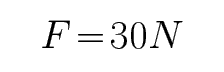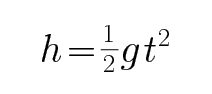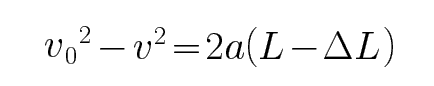- 曲线运动、万有引力
- 共1187题
如图所示，在竖直平面内有半径为R=0.2 m的光滑1/4圆弧AB，圆弧B处的切线水平，O点在B点的正下方，B点高度为h=0.8 m。在B端接一长为L=1.0 m的木板MN。一质量为m=1.0 kg的滑块，与木板间的动摩擦因数为0.2，滑块以某一速度从N点滑到板上，恰好运动到A点。 (g取10 m/s2)求：
29.滑块从N点滑到板上时初速度的大小；
30. 从A点滑回到圆弧的B点时对圆弧的压力；
31．若将木板右端截去长为ΔL的一段，滑块从A端由静止释放后，将滑离木板落在水平面上P点处，要使落地点P距O点最远，ΔL应为多少？
正确答案
解析
由动能定理可知：
代入数据解得：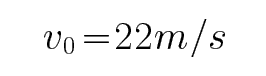
考查方向
动能定理的应用
解题思路
对N到A过程运用动能定理，求出初速度的大小．
易错点
理清物块的运动规律，选择合适的规律进行求解．
正确答案
滑块滑至B点时对圆弧的压力为30 N,方向竖直向下
解析
根据动能定理有：
由向心力公式可知：
联立解得：
由牛顿第三定律知：滑块滑至B点时对圆弧的压力为30 N，方向竖直向下．
考查方向
动能定理的应用
解题思路
根据动能定律求出滑块在B点时的速度，结合牛顿第二定律求出支持力的大小，从而得出滑块对圆弧的压力大小．
易错点
理清物块的运动规律，选择合适的规律进行求解．
正确答案
当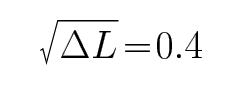
解析
由牛顿第二定律可知：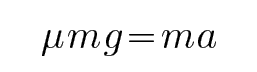
根据平抛运动规律有：
解得：t＝0.4s．
由运动学公式可知：
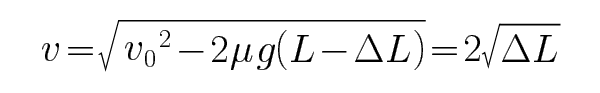
由平抛运动规律和几何关系：
解得当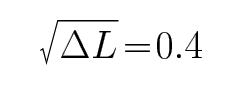
考查方向
动能定理的应用
解题思路
根据牛顿第二定律和运动学公式求出离开木板的速度，结合高度求出平抛运动的时间，从而得出水平位移的表达式，通过数学知识求出△L为多少时，落地点距离O点最远．
易错点
理清物块的运动规律，选择合适的规律进行求解．
如图所示，一光滑弧形轨道末端与一个半径为
12.前车被弹出时的速度
13.前车被弹出的过程中弹簧释放的弹性势能
14.两车从静止下滑处到最低点的高度差
正确答案
解析
设前车在圆轨道的最高点的速度为
前车在最低点位置与后车分离后的速度为
解得：
考查方向
牛顿第二定律；机械能守恒定律
解题思路
前车沿圆环轨道运动恰能越过圆弧轨道最高点，根据牛顿第二定律求出最高点速度，根据机械能守恒列出等式求解.
易错点
前车恰能越过圆弧轨道最高点，说明在最高点只有重力提供前车做圆周运动的向心力.
正确答案
解析
设两车分离前的速度为
分离前弹性势能为
考查方向
动量守恒定律；机械能守恒定律
解题思路
由动量守恒定律求出两车分离前速度，根据系统机械能守恒求解.
易错点
理解弹簧减少的弹性势能等于系统增加的动能.
正确答案
解析
两车从高处运动到最低处机械能守恒
解得：
考查方向
机械能守恒定律
解题思路
两车从h高处运动到最低处机械能守恒列出等式求解．
易错点
掌握机械能守恒的条件.
7．如图6所示，BC是半径为R的竖直面内的圆弧轨道，轨道末端C在网心O的正下方，
∠BOC= 60°，将质量为m的小球，从与O等高的A点水平抛出，小球恰好从B点沿圆弧切线
方向进入网轨道，由于小球与圆弧之间有摩擦，能够使小球从B到C做匀速圆周运动。重力
A从B到C，小球克服摩擦力做功为
B从B到C，小球与轨道之间的动摩擦因数可能保持不变
CA、B两点间的距离为
D在C点，小球对轨道的压力为
正确答案
解析
AC.小球做从A到B做平抛运动，在B点由题可知小球速度方向偏角θ=60°，则
竖直方向的位移:
BD.从B到C，小球对轨道的压力是变化的，而小球仍能保持匀速圆周运动，则小球与轨道之间的动摩擦因数是变化的；在C点，轨道对小球的支持力设为FN，则有
考查方向
动能定理；平抛运动；牛顿第二定律；向心力；牛顿第三定律
解题思路
小球进入轨道前做平抛运动，应用平抛运动规律可以求出小球的初速度，利用小球的水平位移与竖直位移公式，从而求出A、B两点的距离，由牛顿第二定律与牛顿第三定律可以求出小球对轨道的压力.
易错点
关键理解小球恰好从B点沿圆弧切线方向进入轨道的含义，即小球速度方向偏角θ=60°.
知识点
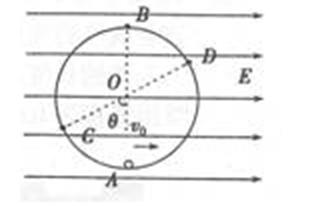
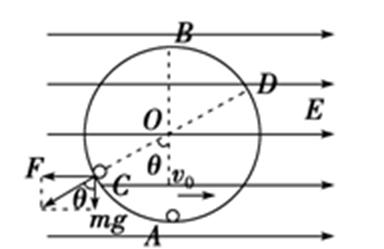
3．如图所示，是两等量同种点电荷Q形成的电场，AB为两电荷连线的中垂线，O为两电荷连线的中点，C为中垂线上的一点，一带电粒子(不计重力)以速度
A带电粒子电性与Q相反
B若该粒子从C点射入电场的速度小于
C若该粒子从C点射入电场的速度大于
D若改变粒子速度大小从中垂线上其他点射入电场，不可能做圆周运动
正确答案
解析
A、根据题意，带电粒子以速度v 0垂直中垂线从C点垂直纸面向里射入电场，恰能绕O点做匀速圆周运动，合力指向O点，带电粒子的电性与Q相反；如果粒子所带电性与两个点电荷相同，合力就背离O点向外，不可能做圆周运动，故A正确；
B、若该粒子从C点射入电场的速度小于V0，所受电场力大于所需要的向心力做近心运动，故B错误；
C、若该粒子从C点射入电场的速度大于v 0 ，所受电场力小于所需要的向心力，做离心运动，故C错误；
D、带电粒子从中垂线上的其他点射入电场，所受电场力大小改变，如果改变速度大小，使得电场力等于所需要的向心力，仍可能做圆周运动，故D错误；
考查方向
电场强度及其叠加；向心力；库仑定律
解题思路
根据等量同种点电荷中垂线上电场的分布特点，如果是两个带正电的点电荷，中垂线上方电场向上，中垂线下方电场向下，绕O点做匀速圆周运动，电场力指向O点，粒子只能带负电；如果是两个带负电的点电荷，中垂线上方电场向下，中垂线下方电场向上，绕O点做匀速圆周运动，电场力指向O点，粒子带正电；粒子速度大于或小于V0，电场力与所需要的向心力不相等，不可能做圆周运动；从中垂线上的其他点射入电场，电场力大小改变，只要改变速度大小，仍可能做圆周运动.
易错点
关键是要熟悉中垂线和连线上电场的分布，知道提供的向心力等于需要的向心力做圆周运动，提供的向心力小于需要的向心力做离心运动，提供的向心力大于所需要的向心力做近心运动.
知识点
数据库的三级模式结构由外模式、模式和内模式组成，其中模式的个数是( )。
A．1个
B．2个
C．3个
D．任意多个
正确答案
A
解析
暂无解析
19．如图所示，在水平转盘上放有两个可视为质点的相同的木块P和Q，两者用长为x的细绳连接，木块与转盘的最大静摩擦力均为各自重力的k倍，P放在距离转轴x处，整个装置能绕通过转盘中心的转轴O1O2转动。开始时，绳恰好伸直但无弹力，现让该装置从静止开始转动，使角速度缓慢增大，以下说法正确的是（ ）
Aω在
B当ω＞
C当ω＞
Dω在0＜ω＜
正确答案
解析
ABC、当Q达到最大静摩擦力时，绳子开始出现弹力，kmg=2mxω2，解得:
当P所受的摩擦力达到最大静摩擦力时，P、Q相对于转盘会滑动，对P有：
kmg-T=mxω2，对Q有：T+kmg=2mxω2，解得：
D、当ω在
考查方向
向心力；线速度、角速度和周期、转速
解题思路
开始角速度较小，两木块都靠静摩擦力提供向心力，由于Q离转轴较远，Q先到达最大静摩擦力，角速度继续增大，则绳子出现拉力，P靠静摩擦力和拉力的合力提供向心力，拉力增大，静摩擦力增大，当增大到最大静摩擦力时，开始发生相对滑动.
易错点
本题的关键搞清木块向心力的来源，结合牛顿第二定律进行分析.
知识点
2．如图所示是男子体操项目中的“单臂大回环”。运动员单手抓住单杠，伸展身体，从静止开始以单杠为轴做圆周运动。已知运动员质量为60kg，若忽略运动过程中空气阻力及手与单杠间摩擦，则运动员到达最低点时手臂所受拉力约为（）
正确答案
解析
设人的长度为L人的重心在人体的中间．最高点的速度最小为零，根据动能定理得：
解得最低点人的速度为
根据牛顿第二定律得：
解得：F=5mg=5×600=3000N．故C正确．
故选：C．
考查方向
动能定理、向心力
解题思路
人在最高点的最小速度为零，根据动能定理求出人在最低点的速度，再根据牛顿第二定律求出拉力的大小．
易错点
关键知道最高点的最小速度为零.
知识点
What are my chances of {{U}}promotion{{/U}} if I stay here
A．retirement
B．advertisement
C．advancement
D．replacement
正确答案
C
解析
[解析] 划线词为名词，意思是“提升，晋级”，与C项advancement(前进；进展)为同义词，又如：The aim of a university should be the advancement of learning．大学的目标应是促进学术的发展。A项意为“退休”，例：She took to painting after retirement．她退休后爱上了绘画。B项意为“广告”，例：Advertisement helps to sell goods．广告有助于推销商品。D项意为“代替”，例：We need a replacement for the secretary who left．我们需要一个人代替已离职的秘书。
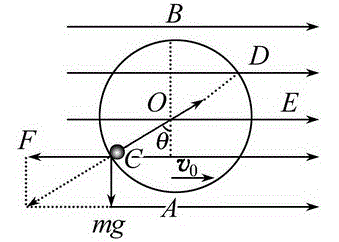
如图所示，在竖直平面内固定的圆形绝缘轨道的圆心在
O点，半径为r，内壁光滑，A、B两点分别是圆形轨道的最低点
和最高点．该区域存在方向水平向右的匀强电场，一质量为m、
带负电的小球在轨道内侧做完整的圆周运动（电荷量不变），经过
C点时速度最大，O、C连线与竖直方向的夹角θ=60°，重力加
速度为g．求：
26.小球受到的电场力的大小；
27.小球在A点的速度vo多大时，小球经过B点时对轨道的压力最小？
正确答案
F＝mg. （2分）
解析
小球经过C点时速度最大，则在该点电场力与重力的合力沿半径方向，小球受到的电场力的大小 F＝mgtan 60° （2分）
F＝mg. （2分）
考查方向
带电粒子在匀强电场中的运动
解题思路
抓住带电小球运动至C点的速度最大这一突破口，竖直面内圆周运动的最大速度出现在物理“最低点”，即合外力沿半径指向圆心，而电场力和重力的合力则背离圆心的方向
易错点
小球经C点时速度最大这也关键突破口展开讨论
正确答案
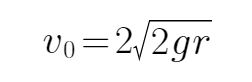
解析
小球经过B点时对轨道的压力最小，则需小球到达D点时速度最小．设小球在D点时轨道对小球的压力恰好为零，
有
＝m （ 2分）
v＝ （ 2分）
在小球在轨道上由A点运动到D点的过程中有：
mg·r(1＋cos θ)＋F·rsin θ＝mv－mv2 （ 4分）
解得：v0＝2. （2分）
考查方向
带电粒子在匀强电场中的运动
解题思路
竖直面内圆周运动的最高点，轨道对小球的压力竖直向下，对B的压力最小时，对D的最小压力等于零．
易错点
小球在B点压力对轨道压力最小为0，根据指向圆心的合力提供圆周运动向心力为解题关键．
在市场经济条件下，政府可界定在( )方面来矫正市场失灵的作用范围。
A．提供公共物品或服务
B．矫正外部效应
C．维持有效竞争
D．调节收入分配
E．直接参与市场运行
正确答案
A,B,C,D
解析
[解析] 在市场经济条件下，政府可界定在以下5个方面来矫正市场失灵作用范围：(1)政府有必要解决提供公共产品或服务的问题；(2)政府有责任纠正外部效应的问题；(3)政府需要承担维持市场有效竞争的责任；(4)政府有义务解决收入分配不公的问题；(5)政府有必要干预市场经济的运行，从而稳定经济，保证其健康地发展。故本题答案为ABCD。
扫码查看完整答案与解析