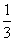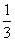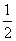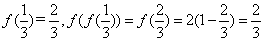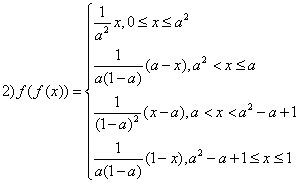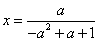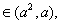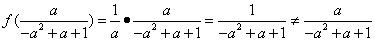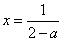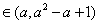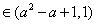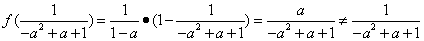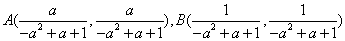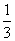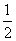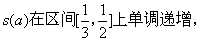- 直线的一般式方程与直线的平行关系
- 共1题
1
题型:简答题
|
设函数

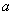
(1)当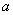
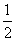

(2)若x0满足f(f(x0))= x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点,证明函数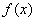
(3)对于(2)中x1,x2,设A(x1,f(f(x1))),B(x2,f(f(x2))),C(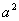
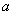
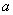


正确答案
见解析
解析
(1)当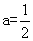
(
当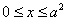
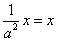
当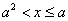
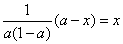
因
故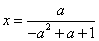
当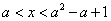
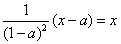
因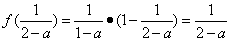
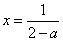
当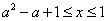
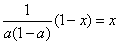
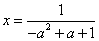
因
故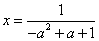
因此,函数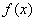
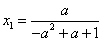
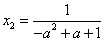
(3)由(2)得
则
因为a在[

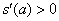
故
知识点
直线的一般式方程与直线的平行关系
下一知识点 : 待定系数法求直线方程
扫码查看完整答案与解析