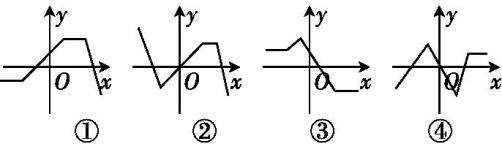
- 函数的图象
- 共20题
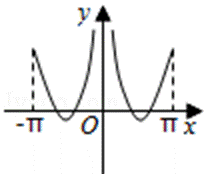
12.如图,偶函数






正确答案
解析
由图象可知f(x)=0有三个根,0,
由图象可知,g(x)所对的每一个值都能有3个根,因此m=9,同理可得,n=9,所以选A.
考查方向
解题思路
结合函数图象把方程根的个数转化为函数图象的交点
个数,可分别求出m.n,进而得到答案
易错点
数型结合思想的相互转化错误
知识点
5.函数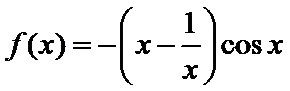
正确答案
解析
试题分析:根据函数的奇偶性判断出函数图象的对称性,利用0<x<1时函数值的正负进一步排除得出答案。
对于函数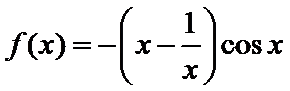
且满足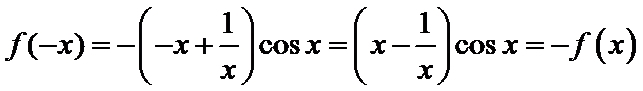
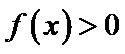
考查方向
解题思路
由条件可得函数f(x)为奇函数,故它的图象关于原点对称;再根据但是当x趋向于0时,f(x)>0,结合所给的选项,得出结论.
易错点
判断函数的奇偶性首先要看函数的定义域.
知识点
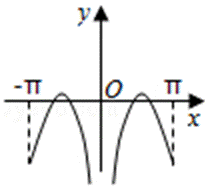
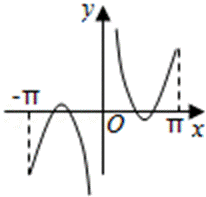
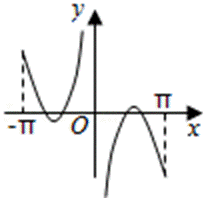
6.下列四个函数图象,只有一个是符合y=|k1x+b1|+|k2x+b2|-|k3x+b3|(其中k1,k2,k3为正实数,b1,b2,b3为非零实数)的图象,则根据你所判断的图象,k1,k2,k3之间一定成立的关系是( )
正确答案
解析
当x足够小时,y=-(k1+k2-k3)x-(b1+b2-b3)
当x足够大时,y=(k1+k2-k3)x+(b1+b2-b3)
可见折线的两端的斜率必定为相反数,此时只有③符合条件.
此时k1+k2-k3=0.
知识点
6.设定义域为R的函数f(x)=
正确答案
解析
作出f(x)的图象(图略),图象关于x=2对称
且当x=2时,f(x)=1,
故f(x)=1有三个不同实数根x
除此之外,f(x)只有两个根或无根.
又f2(x)+af(x)+b=0有三个不同的实数解x1<x2<x3,x2=2,而x1+x3=2x2=4.
又当x≠2时,f(x)=
故A,B,C正确.
知识点
13.如图所示,函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析