- 立体几何中的向量方法
- 共7934题
如图所示,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,AB=2,PA=2
(1)求证:平面PCD∥平面MBE;
(2)设PA=λAB,当二面角D-ME-F的大小为135°,求λ的值.
正确答案

∵M是PA的中点,∴MG∥PD
∵PD⊄平面MBE,MG⊂平面MBE
∴PD∥平面MBE
∵DC∥BE,DC⊄平面MBE,BE⊂平面MBE
∴DC∥平面MBE
∵PD∩DC=D
∴平面PCD∥平面MBE;
(2)解:不妨设AB=2,则PA=2λ,在正六边形ABCDEF中,连接AE,过点F作FH⊥AE,垂足为H,则FH=AFsin∠FAE=1,AH=AFcos∠FAE=




∴




设平面DME的法向量为
由


同理可得平面FME的法向量为
∴
∵二面角D-ME-F的大小为135°
∴
∴λ2=6
∵λ>0,
∴
解析

∵M是PA的中点,∴MG∥PD
∵PD⊄平面MBE,MG⊂平面MBE
∴PD∥平面MBE
∵DC∥BE,DC⊄平面MBE,BE⊂平面MBE
∴DC∥平面MBE
∵PD∩DC=D
∴平面PCD∥平面MBE;
(2)解:不妨设AB=2,则PA=2λ,在正六边形ABCDEF中,连接AE,过点F作FH⊥AE,垂足为H,则FH=AFsin∠FAE=1,AH=AFcos∠FAE=




∴




设平面DME的法向量为
由


同理可得平面FME的法向量为
∴
∵二面角D-ME-F的大小为135°
∴
∴λ2=6
∵λ>0,
∴

(Ⅰ)当E是AB的中点时,求证:AF∥平面PEC;
(Ⅱ)要使二面角P-EC-D的大小为45°,试确定E点的位置.
正确答案

(I)证明:如图,取PC的中点O,连接OF,OE.
由已知得OF∥DC且
又∵E是AB的中点,则OF∥AE且OF=AE,
∴AEOF是平行四边形,
∴AF∥OE
又∵OE⊂平面PEC,AF⊄平面PEC
∴AF∥平面PEC.
(II)解:如图,作AM⊥CE交CE的延长线于M.
连接PM,由三垂线定理得PM⊥CE,
∴∠PMA是二面角P-EC-D的平面角.
∴∠PMA=45°,
∵PA=1,∴AM=1,
设AE=x,
由△AME≌△CBE,得

故要使二面角P-EC-D的大小为45°,只需
解法二:
(I)证明:由已知,AB,AD,AP两两垂直,
分别以它们所在直线为x,y,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),
∴
∵E(1,0,0),C(2,1,0),P(0,0,1),
设平面PEC的法向量为
则


由

又AF⊄平面PEC,故AF∥平面PEC.
(II)解:由已知可得平面DEC的一个法向量为
设E=(t,0,0),设平面PEC的法向量为
则

由
故,要使要使二面角P-EC-D的大小为45°,只需
解析

(I)证明:如图,取PC的中点O,连接OF,OE.
由已知得OF∥DC且
又∵E是AB的中点,则OF∥AE且OF=AE,
∴AEOF是平行四边形,
∴AF∥OE
又∵OE⊂平面PEC,AF⊄平面PEC
∴AF∥平面PEC.
(II)解:如图,作AM⊥CE交CE的延长线于M.
连接PM,由三垂线定理得PM⊥CE,
∴∠PMA是二面角P-EC-D的平面角.
∴∠PMA=45°,
∵PA=1,∴AM=1,
设AE=x,
由△AME≌△CBE,得

故要使二面角P-EC-D的大小为45°,只需
解法二:
(I)证明:由已知,AB,AD,AP两两垂直,
分别以它们所在直线为x,y,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),
∴
∵E(1,0,0),C(2,1,0),P(0,0,1),
设平面PEC的法向量为
则


由

又AF⊄平面PEC,故AF∥平面PEC.
(II)解:由已知可得平面DEC的一个法向量为
设E=(t,0,0),设平面PEC的法向量为
则

由
故,要使要使二面角P-EC-D的大小为45°,只需

(I )求证:AC丄 PB;
(II)求二面角C-PA-M的大小.
正确答案

(II)用向量法求解:作PM⊥BC,垂足为M,在平面ABC内过点M作MQ⊥BC垂足为M,∵平面PBC丄平面ABC,PM,MQ,BC两两垂直,如图建立空间坐标系M-xyz,其中M为坐标原点.
∵三角形PBC是边长为a的正三角形,,∠ABC=90°,∠BAC=30°,M是BC的中点,
∴A(


∴


设平面MPA的法向量为

不妨令y=
设平面CAP的方向向量为

不妨令z=
∴cos<

∴二面角的大小是arccos
解析

(II)用向量法求解:作PM⊥BC,垂足为M,在平面ABC内过点M作MQ⊥BC垂足为M,∵平面PBC丄平面ABC,PM,MQ,BC两两垂直,如图建立空间坐标系M-xyz,其中M为坐标原点.
∵三角形PBC是边长为a的正三角形,,∠ABC=90°,∠BAC=30°,M是BC的中点,
∴A(


∴


设平面MPA的法向量为

不妨令y=
设平面CAP的方向向量为

不妨令z=
∴cos<

∴二面角的大小是arccos
已知


正确答案
解析
解:∵
∴cos<

则


故选C



正确答案
解析
解:根据题意:∠A=120°,
∴


故选D

(Ⅰ)求证:EF∥平面PAB;
(Ⅱ)求直线BE与平面PAB所成角的正弦值.
正确答案

∵E,F分别是PD,BC的中点,
∴EM∥PA,MF∥AB
∵EM∩MF=M,PA∩AB=A
∴平面EMF∥平面PAB
∵EF⊂平面EMF
∴EF∥平面PAB;
(Ⅱ)解:∵二面角P-CD-A为直二面角,AD⊥DC
∴AD⊥平面PDC
∵PD⊂平面PDC,∴PD⊥AD
∵PD⊥DC,AD∩DC=D
∴PD⊥平面ABCD
设E到平面PAB的距离为h,连接BD,则BD=3
∵PD=4,∴PB=
∵PA=5,AB=3,∴PA⊥AB,∴
∵
∴由等体积可得:

∴直线BE与平面PAB所成角的正弦值为

解析

∵E,F分别是PD,BC的中点,
∴EM∥PA,MF∥AB
∵EM∩MF=M,PA∩AB=A
∴平面EMF∥平面PAB
∵EF⊂平面EMF
∴EF∥平面PAB;
(Ⅱ)解:∵二面角P-CD-A为直二面角,AD⊥DC
∴AD⊥平面PDC
∵PD⊂平面PDC,∴PD⊥AD
∵PD⊥DC,AD∩DC=D
∴PD⊥平面ABCD
设E到平面PAB的距离为h,连接BD,则BD=3
∵PD=4,∴PB=
∵PA=5,AB=3,∴PA⊥AB,∴
∵
∴由等体积可得:

∴直线BE与平面PAB所成角的正弦值为


(Ⅰ)求证:PA∥平面BFD;
(Ⅱ)求二面角C-BF-D的余弦值.
正确答案

∵ABCD是菱形,∴O是AC的中点.…(2分)
∵点F为PC的中点,∴OF∥PA.…(3分)
∵OF⊂平面BFD,PA⊄平面BFD,∴PA∥平面BFD.…(6分)
(Ⅱ)解:如图,以点A为坐标原点,线段BC的垂直平分线所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,令PA=AD=AC=1,
则


∴
设平面BCF的一个法向量为
由



令x=1,则

∵PA⊥平面ABCD,AC⊂平面ABCD,
∴PA⊥AC.
∵OF∥PA,∴OF⊥AC.
∵ABCD是菱形,∴AC⊥BD.
∵OF∩BD=O,∴AC⊥平面BFD.
∴


∴
∴二面角C-BF-D的余弦值是
解析

∵ABCD是菱形,∴O是AC的中点.…(2分)
∵点F为PC的中点,∴OF∥PA.…(3分)
∵OF⊂平面BFD,PA⊄平面BFD,∴PA∥平面BFD.…(6分)
(Ⅱ)解:如图,以点A为坐标原点,线段BC的垂直平分线所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,令PA=AD=AC=1,
则


∴
设平面BCF的一个法向量为
由



令x=1,则

∵PA⊥平面ABCD,AC⊂平面ABCD,
∴PA⊥AC.
∵OF∥PA,∴OF⊥AC.
∵ABCD是菱形,∴AC⊥BD.
∵OF∩BD=O,∴AC⊥平面BFD.
∴


∴
∴二面角C-BF-D的余弦值是

(1)求证:AE⊥平面BCD;
(2)求平面AEF与平面ADC所成的锐角二面角的余弦值;
(3)在线段AF上是否存在点M使得EM∥平面ADC?若存在,请指出点M的位置;若存在,请指出点M的位置;若不存在,说明理由.
正确答案
(Ⅰ)证明:在Rt△ABC中,∠ABC=90°,D为AC的中点,
∴AD=BD=DC,
又∠BAC=60°,
∴△ABD为等边三角形,
∵E是BD的中点,∴AE⊥BD,
∵平面ABD⊥平面BCD,交线为BD,
又在△ABD中,AE⊥BD于E,AE⊂平面ABD
∴AE⊥平面BCD.

由题意知EF⊥BD,又AE⊥BD.
如图,以E为坐标原点,分别以EF,ED,EA所在直线为x轴,y轴,z轴,建立空间直角坐标系E-xyz,
由(Ⅰ)知AB=BD=DC=AD=2,BE=ED=1.
由图1条件计算得则AE=


则E(0,0,0),D(0,1,0),A(0,0,


则

易知,平面AEF的一个法向量为
设平面ADC的法向量为
则
令z=1,得y=
即

∴cos<



即平面AEF与平面ADC所成的锐角二面角的余弦值为
(Ⅲ)解:设
∵
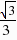

∴


∴


由

解得
∴在线段AF上是否存在点M使得EM∥平面ADC且AM:AF=3:4.
解析
(Ⅰ)证明:在Rt△ABC中,∠ABC=90°,D为AC的中点,
∴AD=BD=DC,
又∠BAC=60°,
∴△ABD为等边三角形,
∵E是BD的中点,∴AE⊥BD,
∵平面ABD⊥平面BCD,交线为BD,
又在△ABD中,AE⊥BD于E,AE⊂平面ABD
∴AE⊥平面BCD.

由题意知EF⊥BD,又AE⊥BD.
如图,以E为坐标原点,分别以EF,ED,EA所在直线为x轴,y轴,z轴,建立空间直角坐标系E-xyz,
由(Ⅰ)知AB=BD=DC=AD=2,BE=ED=1.
由图1条件计算得则AE=


则E(0,0,0),D(0,1,0),A(0,0,


则

易知,平面AEF的一个法向量为
设平面ADC的法向量为
则
令z=1,得y=
即

∴cos<



即平面AEF与平面ADC所成的锐角二面角的余弦值为
(Ⅲ)解:设
∵
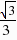

∴


∴


由

解得
∴在线段AF上是否存在点M使得EM∥平面ADC且AM:AF=3:4.

(1)设P是棱BB1的中点,证明:CP∥平面AEB1;
(2)求AB的长;
(3)求二面角B-AB1-E的余弦值.
正确答案
(1)证明:取AB1的中点M,连结PM,ME.
则PM∥BA∥CE,
即四边形PCEM是平行四边形,所以PC∥EM.
又EM⊂平面AEB1,PC⊄平面AEB1.
∴CP∥平面AEB1;
(2)解:由题意
点E到平面AB1A1的距离是AD=3,
所以
(3)解:以A为坐标原点,分别以AB,AD,AA1所在直线为x轴,y轴,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),B1(6,0,2),E(3,3,0),

设平面AB1E的法向量为
由

所以
由平面ABB1的一个法向量为
并设二面角B-AB1-E的大小为α,
则cosα=


所以二面角B-AB1-E的余弦值为
解析
(1)证明:取AB1的中点M,连结PM,ME.
则PM∥BA∥CE,
即四边形PCEM是平行四边形,所以PC∥EM.
又EM⊂平面AEB1,PC⊄平面AEB1.
∴CP∥平面AEB1;
(2)解:由题意
点E到平面AB1A1的距离是AD=3,
所以
(3)解:以A为坐标原点,分别以AB,AD,AA1所在直线为x轴,y轴,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),B1(6,0,2),E(3,3,0),

设平面AB1E的法向量为
由

所以
由平面ABB1的一个法向量为
并设二面角B-AB1-E的大小为α,
则cosα=


所以二面角B-AB1-E的余弦值为

(1)当点C在圆周上运动时,求P的最大值;
(2)记平面A1ACC1与平面B1OC所成的角为θ(0°<θ≤90°),当P取最大值时,求sinθ的值.
正确答案
解:(1)设圆柱的底面半径为r,则AB=AA1=2r,故三棱柱ABC-A1B1C1的体积为
V1=
所以AC•BC≤

从而V1≤2r3,而圆柱的体积V=πr2•2r=2πr3,
故P=



所以P的最大值是
(2)由(1)可知,P取最大值时,OC⊥AB,于是以O为坐标原点,建立空间直角坐标系O-xyz,
则C(r,0,0),B(0,r,0),B1(0,r,2r),
因为BC⊥平面A1ACC1,所以
设平面B1OC的法向量



取z=1得平面B1OC的一个法向量为
所以cosθ=


故sinθ=
解析
解:(1)设圆柱的底面半径为r,则AB=AA1=2r,故三棱柱ABC-A1B1C1的体积为
V1=
所以AC•BC≤

从而V1≤2r3,而圆柱的体积V=πr2•2r=2πr3,
故P=



所以P的最大值是
(2)由(1)可知,P取最大值时,OC⊥AB,于是以O为坐标原点,建立空间直角坐标系O-xyz,
则C(r,0,0),B(0,r,0),B1(0,r,2r),
因为BC⊥平面A1ACC1,所以
设平面B1OC的法向量



取z=1得平面B1OC的一个法向量为
所以cosθ=


故sinθ=
扫码查看完整答案与解析

































