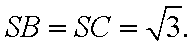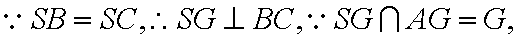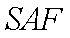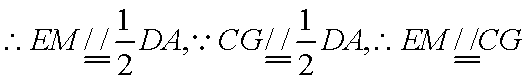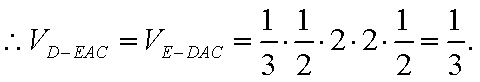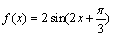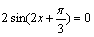- 函数y=Asin(ωx+φ)的应用
- 共30题
18.
在△ABC中,角A,B,C所对的边分别是a,b,c,且
(I)证明:sinAsinB=sinC;
(II)若
正确答案
知识点
8.方程

正确答案
解析





考查方向
解题思路
利用二倍角公式,恒等变形,转化为关于

易错点
换元思想解方程,求角
知识点
11. 已知角





正确答案
解析
根据函数的图象的相邻两条对称轴之间的距离等于






考查方向
解题思路
先求出周期w,再由条件求出
易错点
三角函数周期,同角三角函数转换错误。
知识点
已知函数f(x)=

(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
20.求f(x)的最小周期和最小值,
21.将函数f(x)的图像上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图像.当x
正确答案



解析
试题分析:(Ⅰ)首先用降幂公式将函数


试题解析: (1)

因此


考查方向
解题思路
本题考查三角恒等变形公式及正弦函数的图象及性质,第一问采用先降幂再用辅助角公式将已知函数化为
易错点
三角函数公式的正确运用;
正确答案

解析
试题分析:(Ⅱ)由题目所给变换及(Ⅰ)的化简结果求出函数

试题解析: (2)由条件可知:
当

从而

那么

故


考查方向
解题思路
本题考查三角恒等变形公式及正弦函数的图象及性质,第二小问在第一问的基础上应用三角函数图象变换知识首先求出函数
易错点
三角函数图象变换的性质规律;注意公式的准确性及变换时的符号
8. 若函数




正确答案
解析
f(x)=cos2x-cos(2x+










考查方向
解题思路
先将原函数进行化简整理,f(x)= 


易错点
本小题易在平移过程中出错,忽略x系数2.
知识点
在




(1)求
(2) 若

正确答案
见解析。
解析
(1)因为

又

由


故
(2)由



由余弦定理得
故
知识点
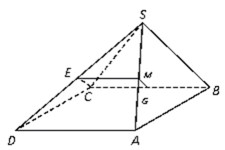
四棱锥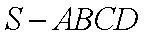
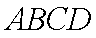
侧面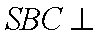
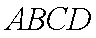
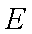
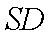
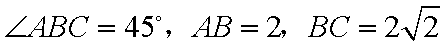
(1)求证: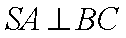
(2)在
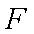
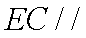
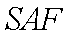
(3)求三棱锥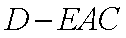
正确答案
见解析。
解析
(1)证明:连接AC, 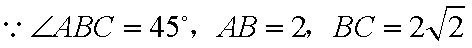
由余弦定理得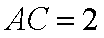
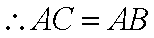
取
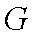
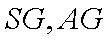
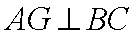

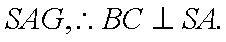
(2)当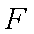

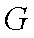
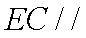
证明:取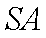
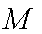
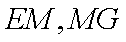
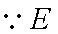
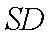

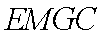
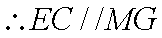
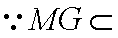
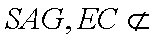
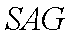

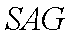
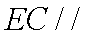
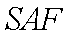
(3)
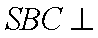
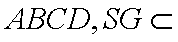
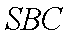
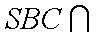
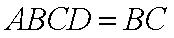
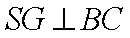
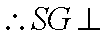
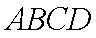
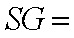
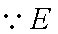
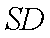
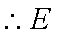
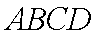
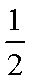
知识点
已知



正确答案
解析
略
知识点
11.已知曲线
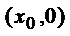


正确答案
解析
利用和差公式求出;
因为关于(x0,0)中心对称。
则,解的x=
考查方向
三角函数的性质。和差公式
解题思路
求出一种三角函数的表达式,利用中心对称必为y0=0,反求出x0
易错点
分清中心对称和轴对称
教师点评
三角函数的考察,抓住三角函数的性质进行解答
知识点
7.将函数





正确答案
解析
考查方向
解题思路
易错点
知识点
扫码查看完整答案与解析