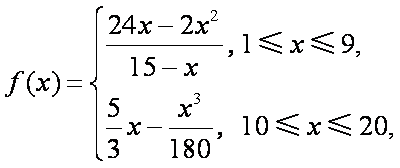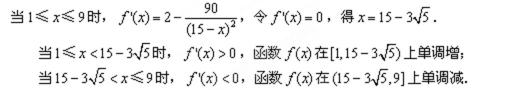- 函数模型的选择与应用
- 共38题
世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形









(1)试用


(2)设矩形









正确答案
(1)

解析
解析:(1)在

所以
矩形


于是
(2) 矩形

又

即草坪造价
由总造价
所以


当且仅当

此时


所以选取

知识点
要制作一个如图的框架(单位:米),要求所围成的面积为6米2,其中ABCD是一个矩形,EFCD是一个等腰梯形,EF=3CD,
(1)求y关于x的表达式;
(2)如何设计x,y的长度,才能使所用材料最少?
正确答案
见解析。
解析
(1)
如图:等腰梯形CDEF中,DH是高
依题意:EH=AB=x米,


∴所求表达式为 
(2)设整个框架用料为l米





当且仅当

此时


知识点
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率
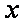
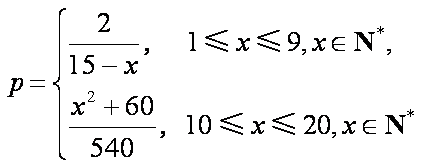

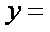
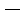
(1)将该车间日利润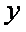
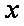
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
正确答案
见解析。
解析
(1)由题意可知,
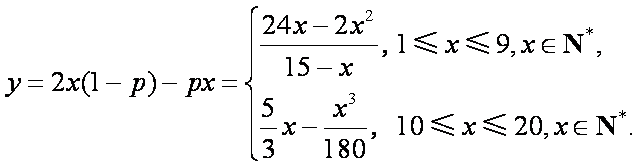
(2)考虑函数
当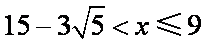
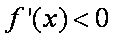
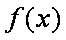
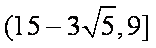
所以当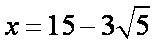
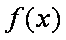
又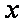
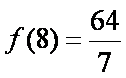
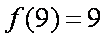
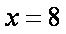
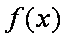
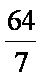
当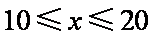
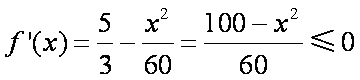

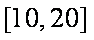
所以当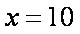
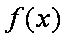

由于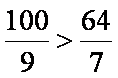
答:当该车间的日产量为10件时,日利润最大,最大日利润是
知识点
甲、乙两地相距1000km,货车从甲地匀速行驶到乙地,速度不得超过80km/h,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
(1)将全程运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,货车应以多大的速度行驶?
正确答案
见解析。
解析
(1)依题意知汽车从甲地匀速行驶到乙地所用时间为
全程运输成本为y=

(2)依题意知a,v都为正数,故有1000(



①若2

②若2

∴函数在v∈(0,80]上单调递减,也即当v=80时,全程运输成本y最小,
综上知,为使全程运输成本y最小,当0<a≤1600时行驶速度应为v=2
知识点
小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元,小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售收入为25﹣x万元(国家规定大货车的报废年限为10年)。
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小张获得的年平均利润最大?(利润=累计收入+销售收入﹣总支出)
正确答案
见解析。
解析
(1)设大货车运输到第x年年底,该车运输累计收入与总支出的差为y万元,
则y=25x﹣[6x+x(x﹣1)]﹣50=﹣x2+20x﹣50(0<x≤10,x∈N)
由﹣x2+20x﹣50>0,可得10﹣5
∵2<10﹣5
(2)∵利润=累计收入+销售收入﹣总支出,
∴二手车出售后,小张的年平均利润为

当且仅当x=5时,等号成立
∴小张应当再第5年将大货车出售,能使小张获得的年平均利润最大。
知识点
某企业有两个生产车间分别在A、B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A、B、C中任意两点间的距离均是1km,设∠BDC=α,所有员工从车间到食堂步行的总路程为S。
(1)写出S关于α的函数表达式,并指出α的取值范围;
(2)问食堂D建在距离A多远时,可使总路程S最少?
正确答案
见解析。
解析
(1)在△BCD中,∵
∴

则


(2)
令S'=0,得
当
当
∴当
此时,


知识点
19.请你设计一个LED霓虹灯灯箱.现有一批LED霓虹灯灯箱材料如图所示,ABCD是边长为60 cm的正方形LED散片,边CD上有一以其中点M为圆心,半径为2 cm的半圆形缺损,因此切去阴影部分(含半圆形缺损)所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于空间一点P,正好形成一个正四棱柱形状有盖的LED霓虹灯灯箱,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE= FB=xcm.
(1)用规格长×宽×高=145 cm×145 cm ×75 cm外包装盒来装你所设计的LED霓虹灯灯箱,灯箱彼此间隔空隙至多0.5 cm,请问包装盒至少能装多少只LED霓虹灯灯箱(每只灯箱容积V最大时所装灯箱只数最少)?
(2)若材料成本2元/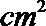
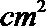

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.某工厂统计资料显示,产品次品率


又知每生产一件正品盈利


(1)将该厂日盈利额

(2)为了获得最大盈利,该厂的日产量应定为多少件?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数p=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 某上市股票在30天内每股的交易价格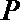

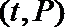
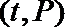
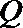
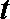
(1)根据提供的图象,写出该种股票每股交易价格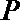
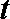
(2)根据表中数据确定日交易量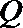

(3)在(2)的结论下,用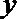
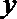
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析