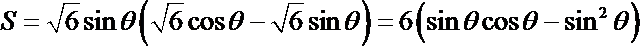- 函数模型的选择与应用
- 共38题
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放



(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放


正确答案
解:(1)因为 

①当



②当



综合得,
(2) 当


由题意知,

因为


故当且仅当


令



又

解析
解析已在路上飞奔,马上就到!
知识点
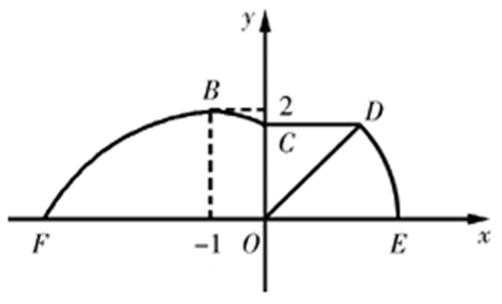
20.如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC.该曲线段是函数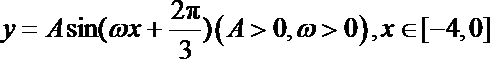


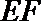
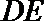
(Ⅰ)求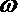
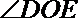
(Ⅱ)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆弧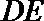
正确答案
(Ⅰ)由条件,得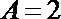
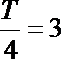
∵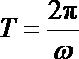
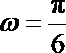
∴ 曲线段FBC的解析式为
当x=0时,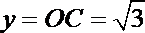
又CD=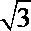
∴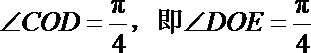
(Ⅱ)由(Ⅰ)知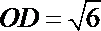
当“矩形草坪”的面积最大时,
点P 在弧DE上,故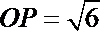
设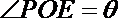
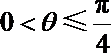
“矩形草坪”的面积为
=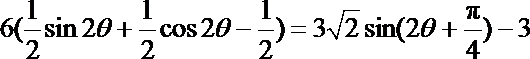
∵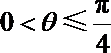
故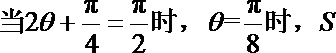
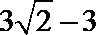
解析
解析已在路上飞奔,马上就到!
知识点
20. 某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率p与日产量x(单位:件,x∈N*)间的关系为
(I)将日利润y(元)表示成日产量x(件)的函数;
(II)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层.每层4000平方米的楼房。经初步估计得知,如果将楼房建为x(x
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
正确答案
解:设楼房每平方米的平均综合费为

法一:
当且仅当
因此,当

为了使楼房每平方米的平均综合费最少,该楼房应建为20层,每平方米的平均综合费最小值为5000元
法二:
解析
解析已在路上飞奔,马上就到!
知识点
17.即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的压力,加速城市之间的流通。根据测算,如果一列火车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次。每天来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,试问每次应拖挂多少节车厢才能使每天营运人数最多?并求出每天最多的营运人数。(注:营运人数指火车运送的人数)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析