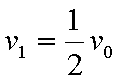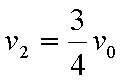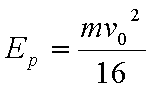- 能量守恒定律与能源
- 共104题
(1)在光电效应试验中,某金属的截止频率相应的波长为



(2)如图,ABC三个木块的质量均为m。置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触可不固连,将弹簧压紧到不能再压缩时用细线把BC紧连,是弹簧不能伸展,以至于BC可视为一个整体,现A以初速

正确答案
见解析。
解析
(1)由

由爱因斯坦质能方程

(2)设碰后A、B和C的共同速度的大小为v,由动量守恒得
设C离开弹簧时,A、B的速度大小为

设弹簧的弹性势能为

由①②③式得弹簧所释放的势能为
知识点
如图,质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上。一电阻不计,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形。棒与导轨间动摩擦因数为μ,棒左侧有两个固定于水平面的立柱。导轨bc段长为L,开始时PQ左侧导轨的总电阻为R,右侧导轨单位长度的电阻为R0。以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向左,磁感应强度大小均为B。在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a。
(1)求回路中感应电动势及感应电流随时间变化的表达式;
(2)经过多长时间拉力F达到最大值,拉力F的最大值为多少?
(3)某过程中回路产生的焦耳热为Q,导轨克服摩擦力做功为W,求导轨动能的增加量。
正确答案
见解析。
解析
(1)感应电动势
导轨做初速为零的匀加速运动,
回路中感应电流随时间变化的表达式
(2)导轨受外力F,安培力

由牛顿定律
上式中,当

(3)设在此过程中导轨运动距离
由于摩擦力

知识点
节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车。有一质量m=1000kg的混合动力轿车,在平直公路上以v1=90km/h匀速行驶,发动机的输出功率为P=50kW。当驾驶员看到前方有80km/h的限速标志时,保持发动机功率不变,立即启动利用电磁阻尼带动的发电机工作给电池充电,使轿车做减速运动,运动L=72m后,速度变为v2=72km/h。此过程中发动机功率的1/5用于轿车的牵引,4/5用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求
(1)轿车以90km/h在平直公路上匀速行驶时,所受阻力F阻的大小;
(2)轿车从90km/h减速到72km/h过程中,获得的电能E电;
(3)轿车仅用其在上述减速过程中获得的电能E电维持72km/h匀速运动的距离L′。
正确答案
见解析。
解析
(1)汽车牵引力与输出功率的关系
将
当轿车匀速行驶时,牵引力与阻力大小相等,有
(2)在减速过程中,注意到发动机只有

电源获得的电能为
(3)根据题设,轿车在平直公路上匀速行驶时受到的阻力仍为

代入数据得
知识点
(1)关于原子核的结合能,下列说法正确的是
a.原子核的结合能等于使其完全分解成自由核子所需的最小能量
b.一重原子核衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于原来重核的结合能
c. 铯原子核(

d.比结合能越大,原子核越不稳定
e.自由核子组成原子核时,其质量亏损所对应的能量大于该原子核的结合能
(2)如图,光滑水平直轨道上有三个质量均为m的物块A、B、C。 B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计)。设A以速度V0朝B运动,压缩弹簧;当A、 B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动。假设B和C碰撞过程时间极短。求从A开始压缩弹簧直至与弹簧分离的过程中,
① 整个系统损失的机械能;
② 弹簧被压缩到最短时的弹性势能。
正确答案
答案:(1)ABC
(2)
(3)
解析
略
知识点
(1)氢原子能级如图,当氢原子从

a. 氢原子从

b. 用波长为325nm的光照射,可使氢原子从

c. 一群处于
d. 用波长为633nm的光照射,不能使氢原子从

(2)如图,光滑水平直轨道上两滑块A.B用橡皮筋连接,A的质量为m。开始时橡皮筋松驰,B静止,给A向左的初速度v0。一段时间后,B与A同向运动发生碰撞并粘在一起。碰撞后的共同速度是碰撞前瞬间A的速度的两倍,也是碰撞前瞬间B的速度的一半。求:
(ⅰ)B的质量;
(ⅱ)碰撞过程中A.B系统机械能的损失。
正确答案
(1)cd
(2)解:
(ⅰ)以初速度v0的方向为正方向,设B的质量为mB,A.B碰撞后的共同速度为v,由题意知:碰撞前瞬间A的速度为

由①式得 
(ⅱ)从开始到碰后的全过程,由动量守恒定律得

设碰撞过程A.B系统机械能的损失为

联立②③④式,得
解析
略。
知识点
某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f,轻杆向右移动不超过l时,装置可安全工作,一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系。
正确答案
见解析。
解析
(1)轻杆开始移动时,弹簧的弹力F=kx①
且F=f②
解得
(2)设轻杆移动前小车对弹簧所做的功为W,则小车从撞击到停止的过程中
由动能定理-f·

同理,小车以vm撞击弹簧时-fl-W=0-
解得
(3)设轻杆恰好移动时,小车撞击速度为v1

由④⑦式解得
当
当

知识点
(1)(4分)2011年3月11日,日本发生九级大地震,造成福岛核电站的核泄漏事故。在泄露的污染物中含有131I和137Cs两种放射性核素,它们通过一系列衰变产
A. 
B.
C. 
D.
(2)(8分)一质量为2m的物体P静止于光滑水平地面上,其截面如图所示。图中ab为粗糙的水平面,长度为L;bc为一光滑斜面,斜面和水平面通过与ab和bc均相切的长度可忽略的光滑圆弧连接。现有一质量为m的木块以大小为v0的水平初速度从a点向左运动,在斜面上上升的最大高度为h,返回后在到达a点前与物体P相对静止。重力加速度为g。求:
(i)木块在ab段受到的摩擦力f;
(ii)木块最后距a点的距离s。
正确答案
(1)B、C;78;82;
(2)(i)
解析
(1)由质量数和核电荷数守恒可以得出正确选项 B C 131I和137Cs原子核中的中子数分别78和82
(2)(i)设木块和物体P共同速度为v,两物体从开始到第一次到达共同速度过程由动量和能量守恒得:


由①②得: 
(ii)木块返回与物体P第二次达到共同速度与第一次相同(动量守恒)全过程能量守恒得:

由②③④得:
知识点
如图所示,质量为






(1)求物块处于平衡位置时弹簧的长度;
(2)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标轴,用
(3)求弹簧的最大伸长量;
(4)为使斜面始终处于静止状态,动摩擦因数
正确答案
见解析
解析
(1)设物块在斜面上平衡时,弹簧伸长量为x,有


(2)由物块所受
得 :
解得:
符合简谐振动的回复力特征,所以是简谐振动.
(3)物块做简谐振动的振幅为

(4)物块运动时,要斜面静止则需要
在物块具有最大向上加速度时保持不动,则整个过程保持不动
联立求解得:
知识点
质量为M的物块静止在光滑水平桌面上,质量为m的子弹以水平速度v0射入物块后,以水平速度2v0/3射出。则物块的速度为____,此过程中损失的机械能为____。
正确答案

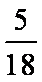
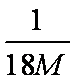
解析
由动量守恒定律,m v0=m·2v0/3+Mv,解得v=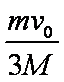
由能量守恒定律,此过程中损失的机械能为△E= 
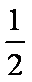
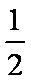
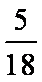
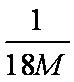
知识点
图18,两块相同平板P1、P2至于光滑水平面上,质量均为m。P2的右端固定一轻质弹簧,左端A与弹簧的自由端B相距L。物体P置于P1的最右端,质量为2m且可以看作质点。P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短,碰撞后P1与P2粘连在一起,P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。
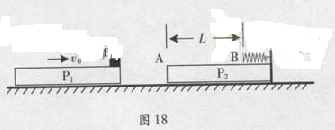
(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2;
(2)此过程中弹簧最大压缩量x和相应的弹性势能Ep
正确答案
见解析
解析
(1)p1和p2碰撞动量守恒:
mv0=(m+m)v1 ①
得出:
P在p2上滑行过程 p1、p2、p系统动量守恒:
2mv0+2mv1=4mv2 ②
得出:
(2)p1 p2 p第一次等速弹簧最大压缩量最大,由能量守恒得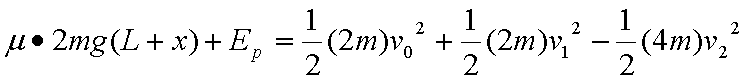
p刚进入p2 到p1 p2 p 第二次等速时有能量守恒得;
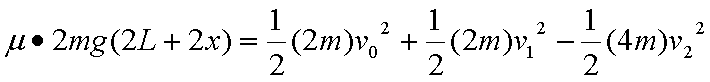
由③④得: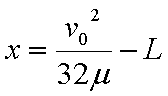
知识点
扫码查看完整答案与解析