- 直线与圆锥曲线
- 共2643题
已知对称中心为坐标原点的椭圆C1与抛物线C2:x2=4y有一个相同的焦点F1,直线l:y=2x+m与抛物线C2只有一个公共点.
(Ⅰ)求直线l的方程;
(Ⅱ)若椭圆C1经过直线l上的点P,当椭圆C1的长轴长取最小值时,求椭圆C1的方程及点P的坐标.
正确答案
解:(Ⅰ)由
∵直线l与抛物线C2只有一个公共点,
∴△=82+4×4m=0,解得m=-4.
∴直线l的方程为y=2x-4;
(Ⅱ)∵抛物线C2的焦点为:F1(0,1),
依题意知椭圆C1 的两个焦点坐标为F1(0,1),F2(0,-1),
如图,
设点F1关于直线l的对称点为
则

∴点
∴直线
直线l与直线

由椭圆的定义及平面几何知识得:
椭圆C1的长轴长2a=
其中当P与P0重合时上式取等号.
∴当a=2时,椭圆的长轴长取得最小值为4,
此时椭圆的方程为

解析
解:(Ⅰ)由
∵直线l与抛物线C2只有一个公共点,
∴△=82+4×4m=0,解得m=-4.
∴直线l的方程为y=2x-4;
(Ⅱ)∵抛物线C2的焦点为:F1(0,1),
依题意知椭圆C1 的两个焦点坐标为F1(0,1),F2(0,-1),
如图,
设点F1关于直线l的对称点为
则

∴点
∴直线
直线l与直线

由椭圆的定义及平面几何知识得:
椭圆C1的长轴长2a=
其中当P与P0重合时上式取等号.
∴当a=2时,椭圆的长轴长取得最小值为4,
此时椭圆的方程为

若AB为抛物线y2=2px (p>0)的动弦,且|AB|=a (a>2p),则AB的中点M到y轴的最近距离是( )
正确答案
解析

抛物线准线为x=-
如图所示:
则所求距离为MN=






所以AB的中点M到y轴的最近距离是
故选D.
已知椭圆C:
正确答案
解析
解:∵△AF2B的周长为16,
∴|AF1|+|BF1|+|AF2|+|BF2|
=4a=16,
解得,a=4;
∵过焦点F1且垂直于长轴的直线被椭圆截得的线段长为2,
∴2
解得,b2=a=4;
故b=2;
则c=

故椭圆C的离心率为e=

故答案为:
椭圆


(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q满足:
正确答案
解:(Ⅰ)由已知得


故所求椭圆C的方程为
(Ⅱ)设A(x1,y1),B(x2,y2),Q(x0,y0)
当λ=0时由

当λ≠0时,设直线AB的方程为y=kx+m.
联立
由△=(4km)2-4(1+2k2)(2m2-2)>0解得m2<1+2k2…(*)
∴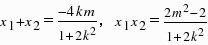

由
∴
代入到

代入(*)式
由1+2k2>0得λ2<4,解得-2<λ<2且λ≠0.
∴综上λ∈(-2,2).
解析
解:(Ⅰ)由已知得


故所求椭圆C的方程为
(Ⅱ)设A(x1,y1),B(x2,y2),Q(x0,y0)
当λ=0时由

当λ≠0时,设直线AB的方程为y=kx+m.
联立
由△=(4km)2-4(1+2k2)(2m2-2)>0解得m2<1+2k2…(*)
∴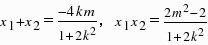

由
∴
代入到

代入(*)式
由1+2k2>0得λ2<4,解得-2<λ<2且λ≠0.
∴综上λ∈(-2,2).





(1)求椭圆C的方程;
(2)过原点且斜率为
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
正确答案
解:(1)因为椭圆C的离心率e=
故设a=2m,c=
直线A2B2方程为 bx-ay-ab=0,
即mx-2my-2m2=0.
所以 

所以 a=2,b=1,椭圆方程为
(2)由

x=




又∵椭圆

∴





∴






∴∠EF2F是锐角
(3)由(1)可知A1(0,1)A2(0,-1),设P(x0,y0),
直线PA1:y-1=

直线PA2:y+1=

解法一:设圆G的圆心为(


则r2=[






OG2=


OT2=OG2-r2=






而
所以OT=2,即线段OT的长度为定值2.…(16分)
解法二:OM•ON=|(-


而
由切割线定理得OT2=OM•ON=4.
所以OT=2,即线段OT的长度为定值2.…(16分)
解析
解:(1)因为椭圆C的离心率e=
故设a=2m,c=
直线A2B2方程为 bx-ay-ab=0,
即mx-2my-2m2=0.
所以 

所以 a=2,b=1,椭圆方程为
(2)由

x=




又∵椭圆

∴





∴






∴∠EF2F是锐角
(3)由(1)可知A1(0,1)A2(0,-1),设P(x0,y0),
直线PA1:y-1=

直线PA2:y+1=

解法一:设圆G的圆心为(


则r2=[






OG2=


OT2=OG2-r2=






而
所以OT=2,即线段OT的长度为定值2.…(16分)
解法二:OM•ON=|(-


而
由切割线定理得OT2=OM•ON=4.
所以OT=2,即线段OT的长度为定值2.…(16分)
点P是椭圆

(1)若点P的坐标为(1,2),求直线AB的方程.
(2)设椭圆的左焦点为F,请问:当点P运动时,∠PFA与∠PFB是否总是相等?若是,请给出证明.
正确答案
解:(1)设点A的坐标为(x1,y1),
当y≥0时,由


则过点A的切线斜率k=y′


又

当y<0时,同理可得切线方程为:
综上,过点A的切线方程为:
∵点P(1,2)在切线上,∴
设点B的坐标为(x2,y2),同理可得,
故由①②可得直线AB的方程为
(2)当点P运动时,∠PFA与∠PFB总是相等的,
F(-1,0),设点P的坐标为(m,n),
则由(1)知,

∵|AF|=2+

=(m+1)(x1+1)+ny1=(m+1)(x1+1)+3(1-
=
∴cos∠PFA=

同理,cos
∴cos∠PFA=cos∠PFB,
∴∠PFA=∠PFB.
解析
解:(1)设点A的坐标为(x1,y1),
当y≥0时,由


则过点A的切线斜率k=y′


又

当y<0时,同理可得切线方程为:
综上,过点A的切线方程为:
∵点P(1,2)在切线上,∴
设点B的坐标为(x2,y2),同理可得,
故由①②可得直线AB的方程为
(2)当点P运动时,∠PFA与∠PFB总是相等的,
F(-1,0),设点P的坐标为(m,n),
则由(1)知,

∵|AF|=2+

=(m+1)(x1+1)+ny1=(m+1)(x1+1)+3(1-
=
∴cos∠PFA=

同理,cos
∴cos∠PFA=cos∠PFB,
∴∠PFA=∠PFB.





(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l平行于AB,与x,y轴分别交于点M,N,与椭圆相交于C,D.证明:△OCM的面积等于△0DN的面积.
正确答案
(Ⅰ)解:依题意,得
解得a=2,b=1. …(3分)
所以椭圆的方程为
(Ⅱ)证明:由于l∥AB,设直线l的方程为y=-

整理得2x2-4mx+4m2-4=0. …(6分)
设C(x1,y1),D(x2,y2).
所以x1+x2=2m,x1x2=2m2-2 …(8分)
记△OCM的面积是S1,△ODN的面积是S2.
由题意M(2m,0),N(0,m),
因为x1+x2=2m,
所以
∵
∴S1=S2 …(14分)
解析
(Ⅰ)解:依题意,得
解得a=2,b=1. …(3分)
所以椭圆的方程为
(Ⅱ)证明:由于l∥AB,设直线l的方程为y=-

整理得2x2-4mx+4m2-4=0. …(6分)
设C(x1,y1),D(x2,y2).
所以x1+x2=2m,x1x2=2m2-2 …(8分)
记△OCM的面积是S1,△ODN的面积是S2.
由题意M(2m,0),N(0,m),
因为x1+x2=2m,
所以
∵
∴S1=S2 …(14分)
椭圆C:

正确答案
(
解析

∵AP⊥0P,∴点P在以AO为直径的圆上,
∵O(0,0),A(a,0),
∴以AO为直径的圆方程为

由
设P(m,n),
∵P、A是椭圆

∴m+a=

∴m=
∵由图形得0<m<a,∴0<
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
∴a<
∴椭圆离心率e=

又∵e∈(0,1),
∴椭圆的离心率e的取值范围为(
故答案为:(
直线l:y=kx-1与双曲线c:2x2-y2=1的左支交于不同的两点,那么k的取值范围是( )
正确答案
解析
解:由
要使y=kx-1与双曲线c:2x2-y2=1的左支交于不同的两点,
则

解①得,-2<k<2.
解②得,

解③得,

所以-2<k<-
故选D.
斜率为2的直线l过双曲线
正确答案
解析


结合图形分析可知,双曲线的一条渐近线的斜率

因此该双曲线的离心率e=

故答案为:
扫码查看完整答案与解析












