- 对数的运算性质
- 共73题
1
题型:填空题
|
9.若
正确答案
10
解析



考查方向
本题考查了对数的运算能力.
解题思路
将右侧的常数转化为同底对数.
易错点
对数的运算性质模糊不清致误.
知识点
对数的运算性质
1
题型:
单选题
|
11.已知函数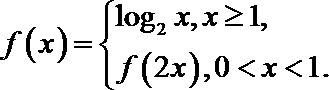
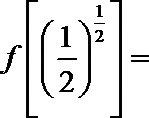
正确答案
B
解析
因为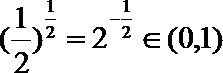
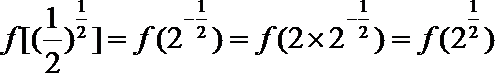

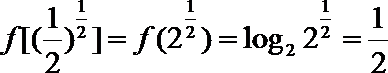
考查方向
本题主要考查了分段函数的求值、对数的运算。
易错点
本题易在判定
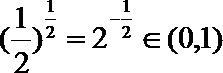
知识点
函数的最值对数的运算性质
1
题型:填空题
|
12.若
正确答案
解析
由指数函数




考查方向
本题主要考查了利用指数函数与对数函数的性质比较大小。
解题思路
本题考查利用指数函数与对数函数的性质比较大小
易错点
本题必须熟知指数函数及对数函数的性质,否则会出现错误。
知识点
指数函数单调性的应用对数的运算性质
1
题型:填空题
|
14.已知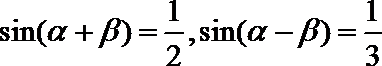

正确答案
1
解析
由题可知,将展开的两式相加减,可求出tana/tanb=5,代入对数式得值为1.
考查方向
本题主要考查了两角和差公式及对数运算
解题思路
本题考查两角和差公式及对数运算,解题思路如下:利用两角和差公式展开已知,两式相加减,求出正切值;代入对数式求解。
易错点
本题必须注意两角和差公式
知识点
对数的运算性质弦切互化两角和与差的余弦函数两角和与差的正弦函数
1
题型:
单选题
|
12.设函数


正确答案
D
解析
∵
∴
易知
∴
考查方向
本题主要考查了分段函数奇偶性和单调性应用
解题思路
先利用分段函数求出g(x),然后判断函数奇偶性,利用单调性进行求解即可
易错点
(1)利用分段函数写出g(x),判断函数的奇偶性
(2)利用单调性解对数不等式
知识点
对数的运算性质其它不等式的解法
下一知识点 : 换底公式的应用
扫码查看完整答案与解析