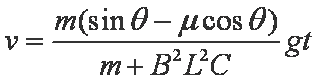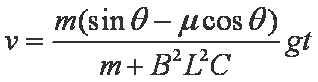- 电磁感应
- 共893题
半径分别为r和2r的同心圆形导轨固定在同一水平面内,一长为r、质量为m且质量分布均匀的直导体棒AB置于圆导轨上面,BA的延长线通过圆导轨中心O,装置的俯视图如图所示,整个装置位于一匀强磁场中,磁感应强度的大小为B,方向竖直向下,在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻(图中未画出),直导体棒在水平外力作用下以速度ω绕O逆时针匀速转动、转动过程中始终与导轨保持良好接触,设导体棒与导轨之间的动摩擦因数为μ,导体棒和导轨的电阻均可忽略,重力加速度大小为g,求:
(1)通过电阻R的感应电流的方向和大小;
(2)外力的功率。
正确答案
(1)在

根据法拉第电磁感应定律,导体棒产生的感应电动势大小为:
根据右手定则,感应电流的方向是从B端流向A端,因此流过导体R的电流方向是从C端流向D端;由欧姆定律流过导体R的电流满足:
联立①②③可得:
(2)
在竖直方向有:
式中,由于质量分布均匀,内外圆导轨对导体棒的正压力相等,其值为N,两导轨对运动的导体棒的滑动摩擦力均为:
在


克服摩擦力做的总功为:
在

根据能量转化和守恒定律,外力在

外力的功率为:
由④至(12)式可得:
解析
略
知识点
如图甲所示,两固定的竖直光滑金属导轨足够长且电阻不计。两质量、长度均相同的导体棒














正确答案
解析
开始c的加速度为














知识点
如图所示,边长为L、不可形变的正方形导体框内有半径为r的圆形区域,其磁感应强度B随时间t的变化关系为B=kt(常量k>0)。回路中滑动变阻器R的最大阻值为R0,滑动片P位于滑动变阻器中央,定值电阻R1=R0、R2=
正确答案
解析
滑片在中间位置是,P将R分为


则R2与










知识点
如图,质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上。一电阻不计,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形。棒与导轨间动摩擦因数为μ,棒左侧有两个固定于水平面的立柱。导轨bc段长为L,开始时PQ左侧导轨的总电阻为R,右侧导轨单位长度的电阻为R0。以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向左,磁感应强度大小均为B。在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a。
(1)求回路中感应电动势及感应电流随时间变化的表达式;
(2)经过多长时间拉力F达到最大值,拉力F的最大值为多少?
(3)某过程中回路产生的焦耳热为Q,导轨克服摩擦力做功为W,求导轨动能的增加量。
正确答案
见解析。
解析
(1)感应电动势
导轨做初速为零的匀加速运动,
回路中感应电流随时间变化的表达式
(2)导轨受外力F,安培力

由牛顿定律
上式中,当

(3)设在此过程中导轨运动距离
由于摩擦力

知识点
如图,两条平行导轨所在平面与水平地面的夹角为θ,间距为L。导轨上端接有一平行板电容器,电容为C。导轨处于匀强磁场中,磁感应强度大小为B,方向垂直于导轨平面。在导轨上放置一质量为m的金属棒,棒可沿导轨下滑,且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ,重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑,求:
(1)电容器极板上积累的电荷量与金属棒速度大小的关系;
(2)金属棒的速度大小随时间变化的关系。
正确答案
(1)Q=CBLv (2)
解析
(1)设金属棒下滑的速度大小为v,则感应电动势为E=BLv①;
平行板电容器两极板之间的电势差为U=E②;
设此时电容器极板上积累的电荷量为Q,按定义有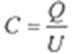
联立①②③式得Q=CBLv④
(2)设金属棒的速度大小为v时经历的时间为t,通过金属棒的电流为I。金属棒受到的电磁场的作用力方向沿导轨向上,大小为f1=BLi④
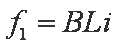
设在时间间隔(t,t+
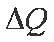
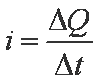


由4式得 
式中,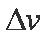
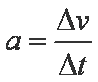
金属棒所受到的摩擦力方向斜向上,大小为
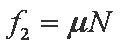
式中,N是金属棒对于轨道的正压力的大小,有
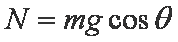
金属棒在时刻t的加速度方向沿斜面向下,设其大小为a,根据牛顿第二定律有
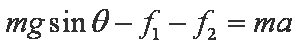
联立5到11式得
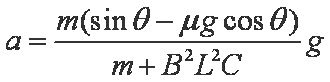
由12式及题设可知,金属棒做初速度为0的匀加速运动。T时刻金属棒的速度大小为
知识点
如图所示,两根足够长的平行金属导轨固定在倾角


(1)cd下滑的过程中,ab中的电流方向;
(2)ab将要向上滑动时,cd的速度v多大;
(3)从cd开始下滑到ab刚要向上滑动的过程中,cd滑动的距离x=3.8m,此过程中ab上产生的热量Q是多少。
正确答案
(1)
(2)
(3)
解析
(1)由
(2)开始放置



设



设电路中的感应电流为

设


此时

综合①②③④⑤式,代入数据解得

(3)设


又

解得

知识点
如图19(a)所示,在垂直于匀强磁场B的平面内,半径为r的金属圆盘绕过圆心O的轴转动,圆心O和边缘K通过电刷与一个电路连接,电路中的P是加上一定正向电压才能导通的电子元件。流过电流表的电流I与圆盘角速度ω的关系如图19(b)所示,期中ab段和bc段均为直线,且ab段过坐标原点。ω>0代表圆盘逆时针转动。已知:R=3.0Ω,B=1.0T,r=0.2m。忽略圆盘、电流表和导线的电阻
(1) 根据图19(b)写出ab、bc段对应I与ω的关系式
(2) 求出图19(b)中b、c两点对应的P两端的电压Ub、Uc
(3) 分别求出ab、bc段流过P的电流Ip与其两端电压Up的关系式
正确答案
见解析
解析
(1)图像得出三点坐标o(0,0)b(15,0.1) c(45,0.4)由直线的两点式得I与ω关系式:
(2)圆盘切割产生的电动势为:
当

Ub=0.3v Uc=0.9v
(3)由并联电路知识有:


由①②得
知识点
如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直纸面,MN、PQ为其边界,OO’为其对称轴。一导线折成边长为
正确答案
解析
正方形闭合回路运动到关于OO’对称的位置时,进出磁感线相同,所以穿过回路的磁通量为零,A正确;根据

知识点
电阻可忽略的光滑平行金属导轨长S=1.15m,两导轨间距L=0.75 m,导轨倾角为30°,导轨上端ab接一阻值R=1.5Ω的电阻,磁感应强度B=0.8T的匀强磁场垂直轨道平面向上。阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热

(1)金属棒在此过程中克服安培力的功
(2)金属棒下滑速度

(3)为求金属棒下滑的最大速度

正确答案
(1)0.4J
(2)3.2m/s2
(3)正确 2.74m/s
解析
(1)下滑过程中安培力的功即为在电阻上产生的焦耳热,由于


(2)金属棒下滑时受重力和安培力

由牛顿第二定律

(3)此解法正确。(1分)
金属棒下滑时舞重力和安培力作用,其运动满足
上式表明,加速度随速度增加而减小,棒作加速度减小的加速运动。无论最终是否达到匀速,当棒到达斜面底端时速度一定为最大。由动能定理可以得到棒的末速度,因此上述解法正确。 (2分)


知识点
某地的地磁场磁感应强度的竖直分量方向向下,大小为4.5×10-5T。一灵敏电压表连接在当地入海河段的两岸,河宽100m,该河段涨潮和落潮时有海水(视为导体)流过。设落潮时,海水自西向东流,流速为2m/s。下列说法正确的是
正确答案
解析
海水在落潮时自西向东流,该过程可以理解为:自西向东运动的导体棒在切割竖直向下的磁场。根据右手定则,右岸即北岸是正极电势高,南岸电势低,D对C错。根据法拉第电磁感应定律E=BLv=4.5×10-5×100×2=9×10-3V, B对A错
知识点
扫码查看完整答案与解析