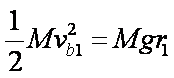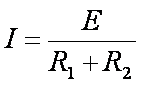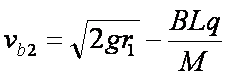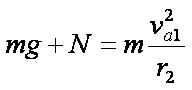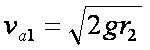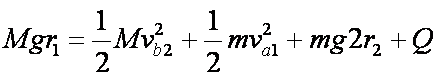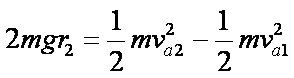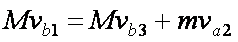- 电磁感应
- 共893题
如图所示,宽度为L的平行光滑的金属轨道,左端为半径为r1的四分之一圆弧轨道,右端为半径为r2的半圆轨道,中部为与它们相切的水平轨道。水平轨道所在的区域有磁感应强度为B的竖直向上的匀强磁场。一根质量为m的金属杆a置于水平轨道上,另一根质量为M的金属杆b由静止开始自左端轨道最高点滑下,当b滑入水平轨道某位置时,a就滑上了右端半圆轨道最高点(b始终运动且a、b未相撞),并且a在最高点对轨道的压力大小为mg,此过程中通过a的电荷量为q,a、b棒的电阻分别为R1、R2,其余部分电阻不计。在b由静止释放到a运动到右端半圆轨道最高点过程中,
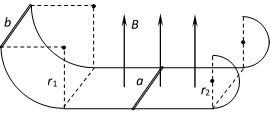
(1)在水平轨道上运动时b的最大加速度是多大?
(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是多少?
(3)a刚到达右端半圆轨道最低点时b的速度是多大?
正确答案
见解析。
解析
(1)由机械能守恒定律:
∴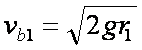
b刚滑到水平轨道时加速度最大,E=BLvb1
F安=BIL=Ma
∴ 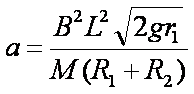
(2)∵ -BILt=Mvb2 –Mvb1 即 -BLq=M vb2 –Mvb1
∴
根据牛顿第三定律得:N=N΄=mg
∴
∵
∴
(3)∵
∴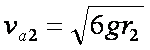
∵
∴
知识点
如图,光滑斜面的倾角为












正确答案
解析
略
知识点
如图所示,两固定竖直光滑金属导轨电阻不计,完全相同的导体棒ab、cd水平置于 匀强磁场上方且相距一定距离。匀强磁场上、下边界水平,方向垂直纸面向里,现同时由静止释放ab、cd,ab进入磁场时恰好做匀速运动,ab出磁场时,cd刚好进入磁场,已知导体棒与导轨接触良好。竖直导轨足够长,则在导体棒cd穿越磁场的过程中
正确答案
解析
略。
知识点
如图,光滑斜面PMNQ的倾角为θ,斜面上放置一矩形导体线框abcd,其中ab边长为l1,bc边长为l2,线框质量为m、电阻为R,有界匀强磁场的磁感应强度为B,方向垂直于斜面向上,e f为磁场的边界,且e f∥MN,线框在恒力F作用下从静止开始运动,其ab边始终保持与底边MN平行,F沿斜面向上且与斜面平行,已知线框刚进入磁场时做匀速运动,则下列判断正确的是
正确答案
解析
略。
知识点
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距













(1)金属棒产生的感应电动势的最大值和电阻
(2)当金属棒速度为向上3m/s时施加在金属棒上外力F的大小和方向?
(3)请求出金属棒在整个运动过程中外力
正确答案
见解析
解析
(1)当速度最大时,感应电动势最大,R上消耗功率最大。
E=BLV0
E =0.4×1×6V=2.4V;
PR=I2R=
(2)当金属棒速度为v=3m/s时,加速度为

由牛顿第二定律得(取沿斜面向下为正方向):

平行于斜面向上
(3) 由图可知速度 
安培力 :
上升阶段由牛顿第二定律:

代入得:F=1.32-0.16t,(0<t<2)
下降时,摩擦力方向改变,安培力随速度改变而改变

知识点
如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m的导体ab垂直于导轨放置,且与两导轨保持良好接触,导体与导轨之间的动摩擦因数为
正确答案
解析
略
知识点
(1)如图所示是氢原子的能级图,大量处于n=4激发态的氢原子向低能级跃迁时,一共可以辐射出6种不同频率的光子,其中巴耳末系是指氢原子由高能级向n=2能级跃迁时释放的光子,则 ( )
A,6种光子中有2种属于巴耳末系
B,6种光子中波长最长的是n=4激发态跃迁到基态时产生的
C,若从n=2能级跃迁到基态释放的光子能使某金属板发生光电效应,则从n=3能级跃迁到n=2能级释放的光子也一定能使该板发生光电效应
D,使n=4能级的氢原子电离至少要0.85eV的能量
E,6种光子中频率最大的是n=4激发态跃迁到基态时产生的
(2)两根足够长的平行光滑导轨,相距1m水平放置。匀强磁场竖直向上穿过整个导轨所在的空间,B=0.4T,金属棒ab、cd质量分别为0.1kg和0.2kg,电阻分别为0.4Ω和0.2Ω,并排垂直横跨在导轨上。若两棒以相同的初速度3m/s向相反方向分开,不计导轨电阻,求:
①棒运动达到稳定时ab棒的速度大小。
②金属棒运动达到稳定的过程中,回路上释放出的焦耳热。
③金属棒运动达到稳定后,两棒间距离增加了多少。
正确答案
答案:(1) ADE
解析
(2) 1ab、cd棒组成的系统动量守恒,最终具有共同速度V,以水平向右为正方 向,则mcdV0 – mabV0 =(mcd + mab)V (2分) V = 1 m/s(1分)
2根据能量转化与守恒定律,产生的焦耳热为:
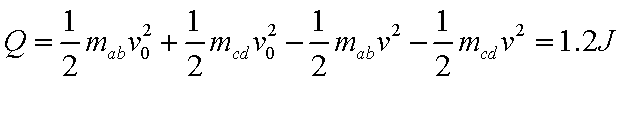
3对cd棒利用动量定理:– BIL·t = mcd(V – V0)
BLq = mcd(V0 – V)
又 q= BLs /(R1 + R2)
s = mcd(V0 – V)(R1+R2)/ B2L2 = 1. 5 m (3分)
知识点
如图所示,MN、PQ是足够长的光滑平行导轨,其间距为L,且MP⊥MN。导轨平面与水平面间的夹角θ=30° 。MP接有电阻R。有一匀强磁场垂直于导轨平面,磁感应强度为B0。将一根质量为m的金属棒ab紧靠MP放在导轨上,且与导轨接触良好,金属棒的电阻也为R,其余电阻均不计。现用与导轨平行的恒力F=mg沿导轨平面向上拉金属棒,使金属棒从静止开始沿导轨向上运动,金属棒运动过程中始终与MP平行。当金属棒滑行至cd处时已经达到稳定速度,cd 到MP的距离为s。
求:
(1)金属棒达到稳定速度的大小;
(2)金属棒从静止开始运动到cd的过程中,电阻R上产生的热量;
(3)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,可使金属棒中不产生感应电流,写出磁感应强度B随时间t变化的关系式。
正确答案
见解析。
解析
(1)当金属棒稳定运动时,

解得: 
(2)由动能定理得:

∴
(3)当回路中的总磁通量不变时,金属棒中不产生感应电流。此时金属棒将沿导轨做匀加速运动。


知识点
如图所示,在倾角为θ的光滑斜面上,存在着两个大小相等、方向相反的匀强磁场,磁场方向与斜面垂直,两磁场的宽度MJ和J G均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场时,线框恰好以速度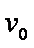
正确答案
解析
略。
知识点
如图,一个方向垂直于纸面向里的匀强磁场,磁场仅限于直角边为L的等腰直角三角形虚线区域内,一固定的每边长为2L正方形金属框,单位长度的电阻为r0,每条边的材料均相同,现让有界匀强磁场沿如图所示方向,以速度v0向右匀速通过金属框,磁场穿过金属框的过程中,下列判断正确的是
正确答案
解析
略。
知识点
扫码查看完整答案与解析