- 电磁感应
- 共893题
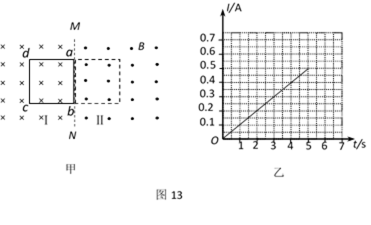
如图（甲）所示，一边长L=2.5m、质量m=0.5kg的单匝正方形金属线框，放在光滑绝缘的水平面上，垂直于水平面的方向上存在着以MN为边界、方向相反的匀强磁场，磁感应强度均为B=0.4T。正方形金属线框的一边ab与MN重合（位置Ⅰ），在力F作用下由静止开始向右平动，经过5s线框刚好被完全拉入另一磁场（位置Ⅱ）。测得金属线框中的电流随时间变化的图象如图（乙）所示，是一条过原点的直线。在金属线框由位置Ⅰ到位置Ⅱ的过程中，
（1）求线框磁通量的变化及感应电动势的平均值；
（2）写出水平力F随时间t变化的表达式；
（3）已知在这5s内力F做功1.5J，那么在此过程中，线框产生的焦耳热是多少？
正确答案
见解析。
解析
（1）△φ＝△B·S＝5Wb
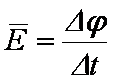
（2）
由电流图像可知，感应电流随时间变化的规律：I=0.1t
由感应电流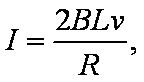
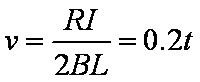
线框在外力F和安培力FA作用下做匀加速直线运动，
F－2BIL ＝ma
得F＝0.2t+0.1（N）
（3）t=5s时，线框从磁场中拉出时的速度v5=at=1m/s
线框中产生的焦耳热Q＝W－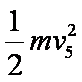
知识点
如图所示，竖直平面内有无限长、不计电阻的两组平行光滑金属导轨，宽度均为L=0.5m，上方连接一个阻值R=1Ω的定值电阻，虚线下方的区域内存在磁感应强度B=2T的匀强磁场。完全相同的两根金属杆1和2靠在导轨上，金属杆与导轨等宽且与导轨接触良好，电阻均为r=0.5Ω。将金属杆1固定在磁场的上边缘（仍在此磁场内），金属杆2从磁场边界上方h0=0.8m处由静止释放，进入磁场后恰作匀速运动。
求：
（1）金属杆2的质量m为多大？
（2）若金属杆2从磁场边界上方h1=0.2m处由静止释放，进入磁场经过一段时间后开始匀速运动。在此过程中整个回路产生了1.4J的电热，则此过程中流过电阻R的电量q为多少？
（3）金属杆2仍然从离开磁场边界h1=0.2m处由静止释放，在金属杆2进入磁场的同时由静止释放金属杆1，两金属杆运动了一段时间后均达到稳定状态，试求两根金属杆各自的最大速度。（已知两个电动势分别为E1、E2不同的电源串联时，电路中总的电动势E=E1+E2。）
正确答案
见解析。
解析
（1）金属杆2进入磁场前做自由落体运动，
vm=
金属杆2进入磁场后受两个力平衡：mg=BIL，
且E=BLvm，
解出m=
（2）金属杆2从下落到再次匀速运动的过程中，能量守恒（设金属杆2在磁场内下降h2）：mg(h1+h2)=
解出h2=
金属杆2进入磁场到匀速运动的过程中，
解出q=
（3）金属杆2刚进入磁场时的速度v=
释放金属杆1后，两杆受力情况相同，且都向下加速运动，合力等于零时速度即最大。
mg=BIL，且
整理得到：v1+ v2=
因为两个金属杆任何时刻受力情况相同，因此任何时刻两者的加速度也都相同，在相同时间内速度的增量也必相同，即：v1-0 =v2- v
代入数据得v2= v1+2……………… ②
②两式联立求出：v1=1m/s，v2=3m/s
知识点
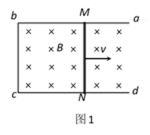
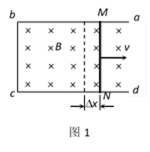
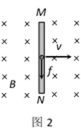
（1）如图1所示，固定于水平面上的金属框架abcd，处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行，bc与ab、dc垂直。MN与bc的长度均为l，在运动过程中MN始终与bc平行，且与框架保持良好接触。磁场的磁感应强度为B。
a. 请根据法拉第电磁感应定律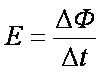
b. 在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E。
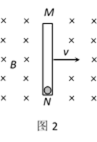
（2）为进一步研究导线做切割磁感线运动产生感应电动势的过程，现构建如下情景：
如图2所示，在垂直于纸面向里的匀强磁场中，一内壁光滑长为l的绝缘细管MN，沿纸面以速度v向右做匀速运动。在管的N端固定一个电量为q的带正电小球（可看做质点）。某时刻将小球释放，小球将会沿管运动。已知磁感应强度大小为B，小球的重力可忽略。在小球沿管从N运动到M的过程中，求小球所受各力分别对小球做的功。
正确答案
见解析。
解析
（1）a. 如图1所示，在一小段时间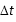
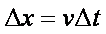
这个过程中线框的面积的变化量
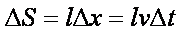
穿过闭合电路的磁通量的变化量
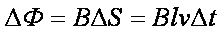
根据法拉第电磁感应定律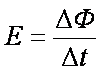 
解得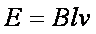 
b. 如图2所示，棒向右运动时，电子具有向右的分速度，受到沿棒向下的洛伦兹力
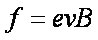
在f的作用下，电子从M移动到N的过程中，非静电力做功
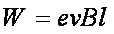
根据电动势定义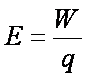 
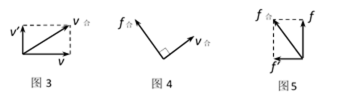
（2）小球随管向右运动的同时还沿管向上运动，其速度如图3所示。小球所受洛伦兹力f合如图4所示。将f合正交分解如图5所示。
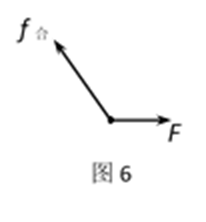
小球除受到洛伦兹力f合外，还受到管对它向右的支持力F，如图6所示。
洛伦兹力f合不做功 
沿管方向，洛伦兹力f做正功
垂直管方向，洛伦兹力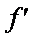
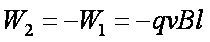
由于小球在水平方向做匀速运动，则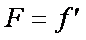 
因此，管的支持力F对小球做正功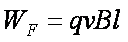 
知识点
在很多情况下，我们对物理规律的理解和认识是通过观察和比较物理现象来进行。在下列的观察及根据观察所得出的响应结论中正确的是
正确答案
解析
略
知识点
如图甲所示，两固定的竖直光滑金属导轨足够长且电阻不计.两质量、长度均相同的导体棒c、d，置于边界水平的匀强磁场上方同一高度h处.磁场宽为3h，方向与导轨平面垂直.先由静止释放c，c刚进入磁场即匀速运动，此时再由静止释放d，两导体棒与导轨始终保持良好接触.用
A
B
C
D
正确答案
解析
略
知识点
电磁感应现象是电磁学中最重大的发现之一，它揭示了电、磁现象之间的本质联系。
电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比，即
（1）如图所示，把矩形线框abcd放在磁感应强度为B的匀强磁场里，线框平面跟磁感线垂直。设线框可动部分ab的长度为L，它以速度v向右匀速运动。请根据法拉第电磁感应定律推导出闭合电路的感应电动势E=BLv。
（2）两根足够长的光滑直金属导轨平行放置在倾角为θ的绝缘斜面上，两导轨间距为L。两导轨间接有阻值为R的电阻。一根质量为m的均匀直金属杆MN放在两导轨上，并与导轨垂直。整套装置处于磁感应强度为B匀强磁场中，磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆MN由静止沿导轨开始下滑。
求
①当导体棒的速度为v（未达到最大速度）时，通过MN棒的电流大小和方向；
②导体棒运动的最大速度。
正确答案
见解析。
解析
（1）在Δt时间内，ab棒向右移动的距离为vΔt，
这个过程中线框的面积变化量是ΔS=LvΔt
穿过闭合回路的磁通量的变化量是
根据法拉第电磁感应定律
（2）①当导体棒的速度为v时，产生的感应电动势为E=BLv
回路中的电流大小为
由右手定则可知电流方向为从N到M
②导体棒在磁场中运动时，所受安培力大小为
由左手定则可知，安培力方向沿斜面向上
当导体棒的加速度为零时，速度最大
即： 
可解得最大速度为
知识点
如图所示，相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场，磁感应强度为B，正方形线圈abcd边长为L（L＜d）,质量为m，电阻为R，将线圈在磁场上方高h处静止释放，cd边刚进入磁场时速度为v0，cd边刚离开磁场时速度也为v0，则线圈穿越磁场的过程中（从cd边刚进入磁场起一直到ab边离开磁场为止），则以下说法中正确的是
A感应电流所做的功为2mgd
B线圈下落的最小速度一定为
C线圈下落的最小速度可能为
D线圈进入磁场和穿出磁场的过程比较，所用的时间不一样
正确答案
解析
略
知识点
如图所示是测量通电螺线管内部磁感应强度的一种装置：把一个很小的测量线圈放在待测处（测量线圈平面与螺线管轴线垂直），将线圈与可以测量电荷量的冲击电流计G串联，当将双刀双掷开关K由位置1拨到位置2时，测得通过测量线圈的电荷量为q。已知测量线圈的匝数为N，截面积为S，测量线圈和G串联回路的总电阻为R。下列判断正确的是：
A在此过程中，穿过测量线圈的磁通量的变化量
B在此过程中，穿过测量线圈的磁通量的变化量
C待测处的磁感应强度的大小为
D待测处的磁感应强度的大小为
正确答案
解析
略
知识点
如图甲所示的电路中，螺线管的匝数
A螺线管中产生的感应电动势为1V
B闭合开关S，电路中的电流稳定后，电阻R1的电功率为
C闭合开关S，电路中的电流稳定后，电容器的下极板带负电
D断开开关S后，一段时间内，流经R2的电流方向由下而上
正确答案
解析
根据法拉第电磁感应定律：E=
知识点
某兴趣小组设计了一种发电装置，如图所示．在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角α均为π，磁场均沿半径方向．匝数为N的矩形线圈abcd的边长ab＝cd＝l、bc＝ad＝2l.线圈以角速度ω绕中心轴匀速转动，bc边和ad边同时进入磁场．在磁场中，两条边所经过处的磁感应强度大小均为B、方向始终与两边的运动方向垂直．线圈的总电阻为r，外接电阻为R。则：
A线圈切割磁感线时，感应电动势的大小Em=2Bl2ω
B线圈切割磁感线时，bc边所受安培力的大小F＝
C线圈旋转一圈时，流过电阻R的净电荷量为零。
D外力做功的平均功率为
正确答案
解析
略
知识点
扫码查看完整答案与解析