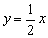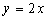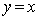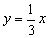- 幂函数的概念、解析式、定义域、值域
- 共682题
1
题型:简答题
|
如图所示,椭圆有两顶点A(-1,0)、B(1,0),过其焦点F(0,1)的直线l与椭圆交于C、D两点,并与x轴交于点P,直线AC与直线BD交于点Q。
(1)当|CD|=时,求直线l的方程;
(2)当点P异于A、B两点时,求证:·为定值。
正确答案
见解析。
解析
知识点
幂函数的概念、解析式、定义域、值域
1
题型:简答题
|
某学校随机抽取了100名学生进行身高调查,得到如下统计表:
(1)求表中a、c、d的值;
(2)根据上面统计表,估算这100名学生的平均身高
(3)若从上面100名学生中,随机选取2名身高不低于185cm的学生,求这2名学生中至少有1名学生身高不低于195cm的概率。
正确答案
见解析。
解析
知识点
幂函数的概念、解析式、定义域、值域
1
题型:
单选题
|
过原点与曲线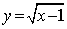
正确答案
A
解析
略
知识点
幂函数的概念、解析式、定义域、值域
1
题型:简答题
|
已知。
(1)化简
(2)若

正确答案
见解析。
解析
(1)
=
(2) 由
所以
=
=
知识点
幂函数的概念、解析式、定义域、值域
1
题型:简答题
|
已知奇函数
(1)求实数
(2)求出函数的单调区间,并指出单调性;
(3)若斜率为k的直线


正确答案
见解析。
解析
(1)因为


所以
因为
(2)因为
所以
又因为
所以

(3)因为
所以
当且仅当



所以当



因为


知识点
幂函数的概念、解析式、定义域、值域
下一知识点 : 幂函数的图像
扫码查看完整答案与解析