圆的切线方程
共533题

· 圆的切线方程

圆的切线方程
共533题

热门试卷

X 查看更多试卷

题型：简答题

简答题

如图，延长⊙O的半径OA到B，使OA=AB，DE是圆的一条切线，E是切点，过点B作DE的垂线，垂足为点C．

求证：∠ACB=∠OAC．

正确答案

解：如图，取EC的中点F，连接AF，OE，AE．

则OE⊥EC，AF∥OE．

∴AF⊥EC．

∴∠CAF=∠EAF．

又∵OE∥AF∥BC，

∴∠EAF=∠OEA=∠OAE，

∠CAF=∠ACB．

∴∠OAE=∠EAF=∠CAF=∠ACB．

∴∠ACB=∠OAC．

解析

解：如图，取EC的中点F，连接AF，OE，AE．

则OE⊥EC，AF∥OE．

∴AF⊥EC．

∴∠CAF=∠EAF．

又∵OE∥AF∥BC，

∴∠EAF=∠OEA=∠OAE，

∠CAF=∠ACB．

∴∠OAE=∠EAF=∠CAF=∠ACB．

∴∠ACB=∠OAC．

题型：填空题

填空题

如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过P点作⊙O的切线，切点为C，连接AC，若∠CPA=30°，PC=______cm．

正确答案

解析

解：连接OC，

PC是⊙O的切线，

∴∠OCP=90°

∵∠CPA=30°，OC==3，

∴tan30°=，

即PC=．

故填：．

题型：简答题

简答题

如图，AB是圆O的直径，AC是弦，∠BAC的平分线AD交圆O于点D，DE⊥AC且交AC的延长线于点E．

求证：DE是圆O的切线．

正确答案

证明：连接OD，

∵OA=OD，∴∠ODA=∠OAD

∵∠BAC的平分线是AD

∴∠OAD=∠DAC

∴∠DAC=∠ODA，可得OD∥AE…（5分）

又∵DE⊥AE，∴DE⊥OD

∵OD是⊙O的半径

∴DE是⊙O的切线．…（10分）

解析

证明：连接OD，

∵OA=OD，∴∠ODA=∠OAD

∵∠BAC的平分线是AD

∴∠OAD=∠DAC

∴∠DAC=∠ODA，可得OD∥AE…（5分）

又∵DE⊥AE，∴DE⊥OD

∵OD是⊙O的半径

∴DE是⊙O的切线．…（10分）

题型：填空题

填空题

如图，AB是⊙O的直径，BC是⊙O的切线，AC与⊙O交于点D，若BC=3，，则AB的长为______．

正确答案

解析

解：∵BC是⊙O的切线，∴BC2=CD•CA，即，CD＞0，解得CD=．

∴AC=5．

由BC是⊙O的切线，∴AB⊥BC．由勾股定理可得==4．

故答案为4．

题型：简答题

简答题

选修4-1：几何证明选讲：

如图，AB为⊙O的直径，D为⊙O上一点且CD⊥AB于C，E，F分别为圆上的点满足∠ACF=∠BCE，直线FE、AB交于P，求证：PD为⊙O的切线．

正确答案

证明：延长FC交圆与G，连接GB、OD，如图．

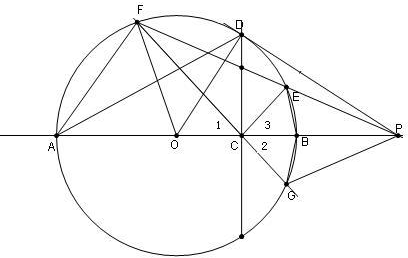
∠POF=2∠OAF，

而∠PEC=∠PEB+∠BEC=∠PAF+∠BGC=∠PAF+∠PAF=2∠PAF，

∴∠POF=∠PEC

又根据圆的对称性，得∠PGC=∠PEC

在△PGC和△FOC中，∠1=∠2，

∠PGC=∠PEC，

∴△PGC∽△FOC，

∴PC•OC=GC•FC，

又CD2=GC•FC，

∴PC•OC=CD2

∴△PDC∽△DOC．

∴∠PDC=∠DOC，

∵∠DOC+∠ODC=90°，

∴∠PDC+∠ODC=90°，

∴PD是⊙O的切线．

解析

证明：延长FC交圆与G，连接GB、OD，如图．

∠POF=2∠OAF，

而∠PEC=∠PEB+∠BEC=∠PAF+∠BGC=∠PAF+∠PAF=2∠PAF，

∴∠POF=∠PEC

又根据圆的对称性，得∠PGC=∠PEC

在△PGC和△FOC中，∠1=∠2，

∠PGC=∠PEC，

∴△PGC∽△FOC，

∴PC•OC=GC•FC，

又CD2=GC•FC，

∴PC•OC=CD2

∴△PDC∽△DOC．

∴∠PDC=∠DOC，

∵∠DOC+∠ODC=90°，

∴∠PDC+∠ODC=90°，

∴PD是⊙O的切线．

继续学习学习下一知识点

下一知识点 : 圆的弦长问题

百度题库 > 高考 > 数学 > 圆的切线方程

扫码查看完整答案与解析