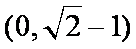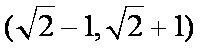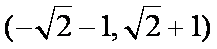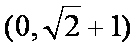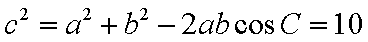- 直线的倾斜角与斜率
- 共186题
如图,已知⊙O是



(1)求证:
(2)过点




正确答案
见解析
解析
(1)证明:连结

所以

则

又

(2)因为

又

因为

则

知识点
过椭圆






正确答案
答案:
解析
由题意知点P的坐标为(-c,



知识点
直线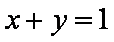
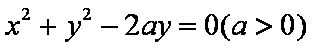
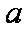
正确答案
解析
因为直线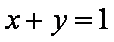
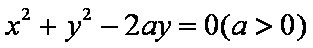

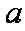
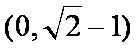
知识点
执行如图的程序,输出的正整数
正确答案
29
解析



知识点
已知直线l:y=2x-2与抛物线M:y=x2的切线m平行
(1)求切线m的方程和切点A的坐标
(2)若点P是直线l上的一个动点,过点P作抛物线M的两条切线,切点分别为B,C,同时分别与切线m交于点E,F试问
正确答案
见解析
解析
解:(1)设切点




(2)设

∵
∴切线


联立方程组

∵点



又∵直线
∴点

又由
∴
∴
又由联立方程组

∴
∴
知识点
已知直线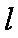

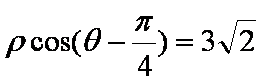
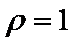

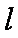
正确答案
解析
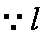
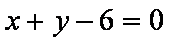

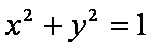
知识点
设
(1)若

(2)确定
正确答案
见解析
解析
(1)由
(2)




在

知识点
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD。
(1)求证:AB∥EF;
(2)求证:平面BCF⊥平面CDEF;
(3)若




正确答案
见解析
解析
(1)因为四边形ABCD是矩形,所以AB∥CD,
因为

所以AB∥平面CDEF,……………………… 4分
因为


所以AB∥EF。
(2)因为DE⊥平面ABCD,
所以DE⊥BC。
因为BC⊥CD,

所以BC⊥平面CDEF。
因为BC
(3)方法一:点E到平面MBD的距离转化为点B到平面MED的距离=
方法二:以D为原点,DA为x轴,DC为y轴,DE为z轴,建系计算得距离=
知识点
在△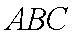
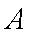
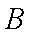
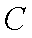
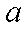
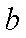

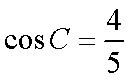
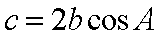
(1)求证: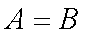
(2)若△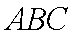
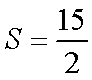

正确答案
见解析
解析
(1)证明:因为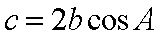
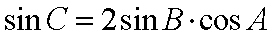
所以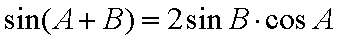
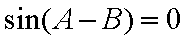
在△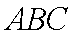
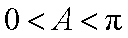
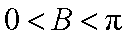
所以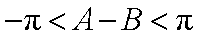
即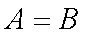
(2)解:由(1)知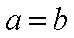
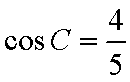
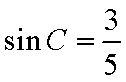
因为△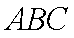
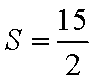
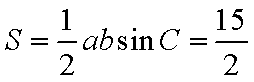
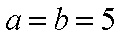
由余弦定理
所以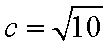
知识点
在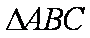


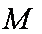
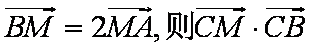
正确答案
解析
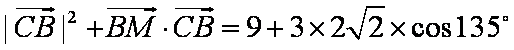
知识点
扫码查看完整答案与解析