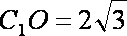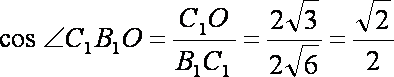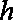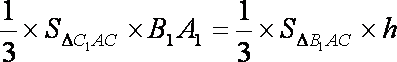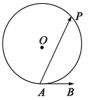- 直线的倾斜角与斜率
- 共186题
直线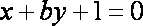
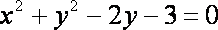
正确答案
-1
解析
圆的方程即为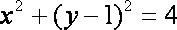
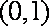
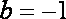
知识点
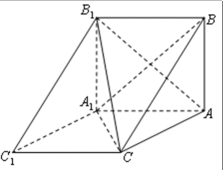
如图,三棱柱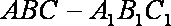
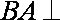

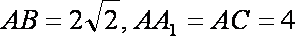
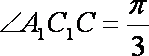
(1)求证: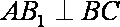
(2)求直线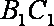
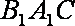
(3)求点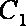
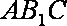
正确答案
见解析
解析
(1)∵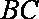
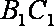
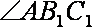
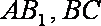
∵ 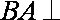
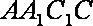
∴ 在直角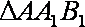
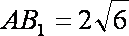
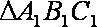
∵ 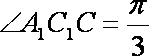
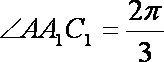
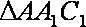
∴ 在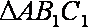
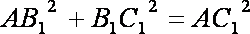
∴
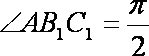
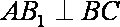
(2)连接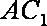
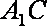

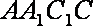
∵ 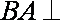
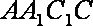
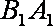
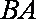
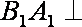
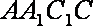
∵ 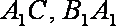
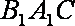

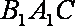
∴ 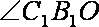
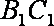
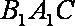
∵ 
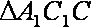
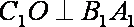
∴ 在直角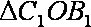
∴ 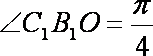

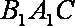
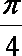
(3)设点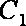
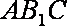
在直角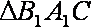
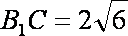
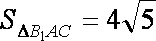
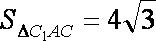
∵ 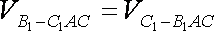
∴
∴ 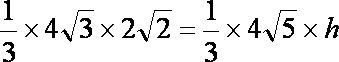
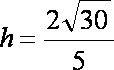
知识点
若直线(m﹣l)x﹣y+2=0与直线3x+my+3=0垂直,则实数m的值等于 。
正确答案
解析
∵直线(m﹣l)x﹣y+2=0与直线3x+my+3=0垂直,∴(m﹣1)3+(﹣1)m=0,解得m=
知识点
如图,在直角梯形








(1)求证:平面

(2)若


正确答案
见解析。
解析
(1) 证明 ∵


又由于
∴正方形

又


因



证法二:又由于



折叠后,




因


(2) ∵





∴点



又∵



由(1)知有




于是,由


∴

又∵



∴
∴
解法(二):也可以体积分割求解,但也应有必要的证明过程。
知识点
已知P是直线

正确答案
2
解析
略
知识点
如图,A是半径为5的圆O上的一个定点,单位向量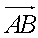

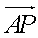
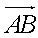
正确答案
[-5,5]
解析
略
知识点
如图,在三棱锥P-ABC中,

(1)求证:AB⊥MN;
(2)求点P到平面NMA的距离.
正确答案
见解析
解析
(1)取AB中点Q,连接MQ、NQ,
∵AN=BN∴
∵


∴
所以AB⊥平面MNQ,又MN
∴AB⊥MN………………6分
(2)设点P到平面NMA的距离为h,
∵


又


∵

又


……………………………………………………………………………9分
可得△NMA边AM上的高为
∴
由
∴
知识点
已知F1(-1,0),F2(1,0)为椭圆C的左、右焦点,且点P(1,
(1)求椭圆C的方程;
(2)过点F1的直线l交椭圆C于A,B两点,问△F2AB的内切圆的面积是否存在最大值?若存在求其最大值及此时的直线方程;若不存在,请说明理由。
正确答案
见解析
解析
解析:(1)由已知,可设椭圆

因为


所以,椭圆
(也可用待定系数法

………………4分
(2)当直线




设


所以
设内切圆半径为





令


又当


故当


………………12分
知识点
如图:四棱锥






(1)证明: 

(2)求点

正确答案
见解析。
解析
(1)证明:因为


所以
所以
又因为

所以

(2)取





由(1)
所以
因为



又因为
所以
所以
又

而

所以
所以点


知识点
如图,



(1)求证:平面EPB
(2)求二面角
正确答案
见解析
解析
解:(1)







(2)过B点作BF






BM为面PAD的斜线,MF为BM在面PAD的射影,


PC与面ABCD成角


BF=

所以二面角B-PD-A平面角正切值为 
知识点
扫码查看完整答案与解析