- 异面直线及其所成的角
- 共54题
如图所示的长方体








(1)求证:

(2)求三棱锥
正确答案
见解析。
解析
(1)
连结
∵




∴四边形
∴
∵



∴

(2)解法1 连结






∴
又∵在长方体



∴



∴

∴



∵
∴
解法2: 三棱锥










知识点
如图,直三棱柱

(1)求直三棱柱
(2)若



正确答案
(1)4(2)
解析
解析:(1)
(2)设





在
即




知识点
如图,四面体







(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)因为CO=

(2)因为O、E为中点,所以OE//CD,所以
AE与CD所成角。
在直角三角形AEO中,
知识点
如图,已知边长为8米的正方形钢板有一个角锈蚀, 其中






正确答案
48
解析
略
知识点
在棱长为





(1)求异面直线

(1)求三棱锥
正确答案
(1)
解析
解析:(1)由题意得


计算


(2)

所以


知识点
如图,已知点








(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)由题意

在△


在△


所以
(2)取




得


又



由余弦定理得
所以异面直线


知识点
如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点,求证:
(1)PA∥平面MDB;
(2)PD⊥BC。
正确答案
见解析。
解析
(1)
连接AC,交BD与点O,连接OM,
∵M为PC的中点,O为AC的中点,
∴MO∥PA,
∵MO⊂平面MDB,PA⊄平面MDB,
∴PA∥平面MDB。
(2)∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC⊂平面ABCD,BC⊥CD,
∴BC⊥平面PCD,
∵PD⊂平面PCD,
∴BC⊥PD。
知识点
如图,四棱锥P—ABCD中,PA


(1)求证:MN//平面PDC;
(2)求三棱锥N—PAC的体积。
正确答案
见解析。
解析
知识点
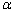
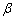
(1)a∥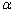
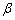
(2)a⊥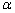
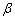
(3)a⊥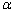
(4)a∥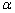
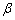
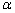
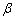
正确答案
解析
由题意知(3)满足条件,∴有一个。
知识点
如图,四棱锥







(1)证明:
(2)证明:

正确答案
见解析。
解析
(1)由



又

(2)
取




又


所以

知识点
扫码查看完整答案与解析