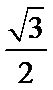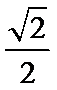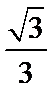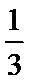异面直线及其所成的角
共54题

· 异面直线及其所成的角

异面直线及其所成的角
共54题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

11.平面过正文体ABCD—A1B1C1D1的顶点A,,，，则m，n所成角的正弦值为（）

正确答案

知识点

余弦定理的应用异面直线及其所成的角

题型：简答题

简答题 · 12 分

19．如图，圆锥的顶点为，底面的一条直径为，为半圆弧的中点，为劣弧的中点.已知，，求三棱锥的体积，并求异面直线与所成角的大小.

正确答案

解析

试题分析：因为，，

所以三棱锥的体积

．

因为，所以异面直线与所成的角就是与的夹角.

在中，，，

过作，则，

在中，，

所以异面直线与所成角的大小.

考查方向

圆锥的性质，异面直线的夹角.

解题思路

求异面直线所成的角常采用“平移线段法”，平移的方法一般有三种类型：利用图中已有的平行线平移；利用特殊点(线段的端点或中点)作平行线平移；补形平移．计算异面直线所成的角通常放在三角形中进行．

易错点

异面直线所成角的寻找

知识点

棱柱、棱锥、棱台的体积异面直线及其所成的角

题型：单选题

单选题 · 5 分

11．平面α过正方体ABCD-A1B1C1D1的顶点A，α//平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，则m，n所成角的正弦值为( )

正确答案

知识点

异面直线及其所成的角直线与平面平行的判定与性质

题型：单选题

单选题 · 5 分

7．设α为平面，a、b为两条不同的直线，则下列叙述正确的是（）

A若a∥α，b∥α，则a∥b

B若a⊥α，a∥b，则b⊥α

C若a⊥α，a⊥b，则b∥α

D若a∥α，a⊥b，则b⊥α

正确答案

解析

对于A答案，直线a与b可以相交，也可以异面，也可以平行；

对于B答案，b和a垂直，但是和平面α的关系不能确定，也可以在平面α内；

对于D答案，b和a垂直，但是和平面α的关系不能确定，可以和平面α斜交。

所以，A选项不正确， C选项不正确，D选项不正确，B选项正确。

考查方向

本题主要考查了立体几何的有关知识：空间中直线与直线的位置关系、直线与平面的位置关系等。

解题思路

1.对每一个选项进行判断即可；

2.也可以画出图形，直接判断。

A选项不正确， C选项不正确，D选项不正确，B选项正确。

易错点

本题在线线平行、线面平行，线线垂直、线面垂直上容易混淆。有些关系没有考虑到导致出错。

知识点

异面直线及其所成的角直线与平面平行的判定与性质直线与平面垂直的判定与性质

题型：简答题

简答题 · 12 分

19．如图,四棱柱的底面是平行四边形,且,,,为的中点, 平面．

（Ⅰ）证明:平面平面；

（Ⅱ）若,试求异面直线与所成角的余弦值．

正确答案

见解析

解析

试题分析：本题属于立体几何中的基本问题，题目的难度是逐渐由易到难．

试题解析：（Ⅰ）依题意∴是正三角形，，

∵⊥平面，平面，

平面

平面，∴平面平面．

（Ⅱ）取的中点，连接、，连接

中，是中位线，,

∴四边形是平行四边形，可得

可得（或其补角）是异面直线与所成的角．

即异面直线与所成角的余弦值为．

考查方向

本题考查了立体几何中的面面垂直和异面直线所成的角的问题．属于高考中的高频考点。

解题思路

本题考查立体几何，解题步骤如下：

（1）转化为证明线面垂直。

（2）找到三角形，利用余弦定理求解。

易错点

（1）第一问中的面面垂直的转化。（2）第二问中异面直线所成的角求解时要找到适当的三角形。

知识点

异面直线及其所成的角直线与平面垂直的判定与性质平面与平面垂直的判定与性质

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 异面直线的判定

百度题库 > 高考 > 文科数学 > 异面直线及其所成的角

扫码查看完整答案与解析