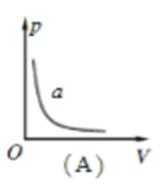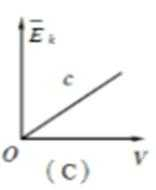- 分子热运动和热机
- 共476题
如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将一定质量的气体封闭在气缸内。在气缸内距缸底60cm处设有a、b两限制装置,使活塞只能向上滑动。开始时活塞搁在a、b上,缸内气体的压强为p0(p0=1.0×105 Pa为大气压强),温度为300K。现缓慢加热汽缸内气体,当温度为330K,活塞恰好离开a、b。求:
(1)活塞的质量
(2)当温度升为360K时活塞上升的高度
正确答案
见解析
解析
p1=1.0×105 Pa, p2=
(1) 
p2=

mg=0.1×105×40×10-4=40N m=4kg
(2) T3=360K V2=V1=60×40cm3
等压变化 

Δh=65.5-60=5.5cm
知识点
(1) 下列说法中正确的有________。
A. 实验“用油膜法估测分子大小”中,油酸分子的直径等于油酸酒精溶液的体积除以相应油酸膜的面积
B. 布朗运动中,悬浮在液体中的固体颗粒越小、液体的温度越高,布朗运动越剧烈
C. 质量、温度都相同的氢气和氧气,分子平均动能不相同
D. 液晶的光学性质与某些晶体相似,具有各向异性
(2)如图所示,粗细均匀的U形管,右端封闭有一段空气柱,两管内水银面高度差为h=19 cm,封闭端空气柱长度为L1=40 cm。为了使左、右两管中的水银面相平,(设外界大气压强p0=76 cmHg, 空气柱温度保持不变)试问:
①需从左管的开口端再缓慢注入多少高度的水银柱?此时封闭端空气柱的长度是多少?
② 注入水银过程中,外界对封闭空气做________(填“正功”或“负功”或“不做功”)气体将________(填“吸热”或“放热”)。
正确答案
(1)BD
(2)①需要再注入39cm的水银柱,空气柱的长度为30cm;②正功;放热
解析
(1)略。
(2)①对空气柱
得L2=30cm
需要再注入39cm的水银柱。
②略。
知识点
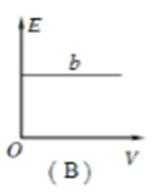
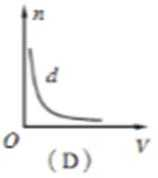
如图,固定的导热气缸内用活塞密封一定质量的理想气体。现用力使活塞缓慢地向上移动。用p、V、E和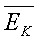
正确答案
解析
略
知识点
(1)关于热现象和热学规律,下列说法中正确的是 .(填正确答案标号.选对一个得3分,选对2个得4分,选对3个得6分.每选错一个扣3分,最低得分为0分)
A.温度升高,每一个分子的热运动速度都增加
B.第二类永动机不可能制造成功的原因是因为能量既不会凭空产生,也不会凭空消失,只能从一个物体转移到另一个物体,或从一种形式转化成另一种形式
C.用活塞压缩气缸里的气体,对气体做了2.0×105J的功,若气体向外界放出1.5×105J的热量,则气体内能增加了0.5×105J
D.利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的
E.内能不同的物体,它们分子热运动的平均动能可能相同
(2)一个密闭的圆柱形气缸竖直放在水平桌面上,缸内有一与底面平行的可上下滑动的活塞将汽缸隔为两部分.活塞导热性能良好,与气缸壁之间无摩擦、不漏气.活塞上方盛有1.5摩尔氢气,下方盛有1摩尔氧气,如图所示.它们的温度始终相同.已知在温度为320K时,氢气的体积是氧气的4倍.试求在温度是多少时氢气的体积是氧气的3倍.
正确答案
(1)CDE
(2)500K
解析
(1)CDE
(2)解析:①设在温度T=320K时,氢气和氧气的体只分别为



已知

将氢气和氧气都看作理想气体,有




设在温度为T´时,氢气的体积为氧气的体积




则有 



因为总体积不变,所以 


因为活塞的质量不变,所以 


可解得 T´=500(开)
知识点
如图所示,内壁光滑的圆柱形玻璃缸竖直放置,缸上端有一抽气孔,缸壁正中央有一卡口C,缸内下部被活塞封住一定质量的理想气体。已知起初气体温度为T1,活塞上方的压强达到p0,此时活塞下方气体的体积为V1,活塞上方缸的容积为2.6V1,活塞因重力而产生的压强为0.5p0。现将活塞上方的气体缓慢抽出(整个抽气过程中缸内气体温度保持不变),活塞上方抽成真空后密封,然后将下方气体缓慢加热。求:
(1)活塞刚到卡口时下方气体的压强p 2;
(2)当下方气体压强为1.6p0时达到的温度T2。
正确答案
见解析
解析
(1)由题意可知,等温过程小水作品
由波义耳定律得:
代入数据
(2)由题意可知,等容过程
由查理定律得:
代入数据得:
知识点
气缸长为L=1m ( 气缸的厚度可忽略不计),开口向上固定在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞质量m=10kg,活塞封闭了一定质量的理想气体,此时气柱长度为L1=0.4 m。已知大气压为p0=1×105Pa。现缓慢拉动活塞,拉力最大值为F=600N,试通过计算判断:保持温度不变,能否将活塞从气缸中拉出? ( 取重力加速度g=10m/ s2)
正确答案
见解析
解析

当拉力达到最大时,

根据波义耳定律:
即:不能将活塞从气缸中拉出
知识点
(1)下列说法正确的是
A.气体对容器的压强是大量气体分子对容器的碰撞引起的,它跟气体分子的密集程度以及气体分子的平均动能有关
B.在绕地球飞行的宇宙飞船中,自由飘浮的水滴呈球形,这是表面张力作用的结果
C.液晶显示器是利用了液晶对光具有各向同性的特点
D.当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小
(2)如图所示的导热气缸固定于水平面上,缸内用活塞密封一定质量的理想气体,外界大气压强保持不变。现使气缸内气体温度从27 ℃缓慢升高到87 ℃,此过程中气体对活塞做功240 J,内能增加了60 J。活塞与气缸间无摩擦、不漏气,且不计气体的重力,活塞可以缓慢自由滑动。
①求缸内气体从外界吸收的热量。
② 升温后缸内气体体积是升温前气体体积的多少倍?
正确答案
(1)AB
(2)1.2倍
解析
(1)略。
(2)①根据热力学第一定律:△E=W+Q 得
Q=△E-W=60J+240J=300J
②根据查理定律:

知识点
如图所示,底面积S= 40cm2的圆柱形气缸C开口向上放置在水平地面上,内有一可自由移动的活塞封闭了一定质量的理想气体,不可伸长的细线一端系在质量为 2kg活塞上,另一端跨过两个定滑轮提着质量为10kg的物体A。开始时,温度t1=7℃,活塞到缸底的距离l1=10cm,物体A的底部离地h1=4cm。已知外界大气压p0=1.0×105Pa不变,现对气缸内的气体缓慢加热直到A物体触地,试问:(重力加速度g=l0m/s2)
(1)开始时气体的压强为多少Pa?
(2)当物体A刚触地时,气体的温度为多少℃?
正确答案
见解析
解析
(1)活塞受力平衡:P0S+mg=P1S+T;T=mAg
被

(2)(初状态:V1=l1s,T1=280K
末状态:V2=(l1+h1)s,T2=?
等压变化,
知识点
(1)下列说法中正确的是
A. 布朗运动就是在显微镜中看到的液体分子的无规则运动
B. 在热机中,燃气的内能不可能全部转化为机械能
C. 一切与热现象有关的宏观自然过程都是有方向的
D. 大颗粒的盐粒磨成细盐,就变成了非晶体
(2)一气缸竖直放置,其横截面积为S=20cm2,气缸内有一个质量不计的活塞,活塞下封闭着一定质量的理想气体,活塞到气缸底的距离L=21 cm,气体的温度t1=7℃,外界大气压强P0=1.0
①在活塞上放一个质量m=0.1kg的砝码,保持气体的温度t1不变,平衡后活塞到气缸底的距离。
②在上述过程中,气体放出的热量。
③保持砝码的质量不变,对气体加热,使其温度升高到t2=77℃,此时活塞到气缸底的距离。
正确答案
(1)BC
(2)①20cm;②2.1J;③25cm
解析
(1)略。
(2)①被封闭气体的初状态为: p1= p0=1.0×105Pa,V1=LS=21S
末态为p2=p0+
根据玻意耳定律,有p1V1=p2V2,即p1L1=p2L2
得
②由热力学第一定律Q=W=p2S(L2-L1)= 2.1J
③对气体加热后,气体的状态变为:V3=L3S,T3=350K
根据盖·吕萨克定律,有
得
知识点
(1)关于热学规律,下列说法正确的是 。(填正确答案标号。选对1个得3分,选对2个得4分,选对3个得6分。每选错1个扣3分,最低得分为0分)
A,热量可以自发地从高温物体向低温物体传递,但要从低温物体向高温物体传递,必须有第三者介入
B,如果用Q表示物体吸收的能量,用W表示物体对外界所做的功,ΔU表示物体内能的增加,那么热力学第一定律可以表达为
C,蒸发的快慢与空气的湿度有关,与气温无关
D,摄氏温度是国际单位制中七个基本物理量之一,摄氏温度t 与热力学温度T的关系是:T=t+273.15K
E,在用油膜法估测分子的直径的实验中,主要是解决两个问题:一是获得很小的一滴油酸并测出其体积,二是测量这滴油酸在水面上形成的油膜面积
(2)用如图所示的装置测量某种矿物质的密度,操作步骤和实验数据如下:
a。打开阀门K,使管A、容器C、容器B和大气相通。上下移动D,使水银面与刻度n对齐;
b。关闭K,向上举D,使水银面达到刻度m处。这时测得B、D两管内水银面高度差h1=19.0cm;
c。打开K,把m=400g的矿物质投入C中,使水银面重新与n对齐,然后关闭K;
d。向上举D,使水银面重新到达刻度m处,这时测得B、D两管内水银面高度差h2=20.6cm。
已知容器C 和管A的总体积为VC=1000cm3,求该矿物质的密度。
正确答案
见解析
解析
(1)ABE
(2)解:设水银的密度为ρ,大气压强为p0,容器B体积为VB,矿物体积V。
以C、A、B中封闭的气体为研究对象,以封闭时水银面处于n处为初状态,以水银面调至m处为末状态。根据玻意耳定律有

以C中装入矿物质后C、A、B中气体为研究对象,以封闭时水银面处于n处为初状态,以水银面调至m处为末状态。根据玻意耳定律有

又
解得
知识点
扫码查看完整答案与解析