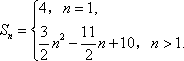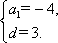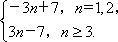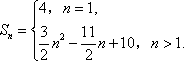数列求和、数列的综合应用
共397题

数列求和、数列的综合应用
共397题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

20.（本小题满分16分）

记.对数列和的子集T，若,定义;若，定义.例如：时，.现设是公比为3的等比数列，且当时，.

(1) 求数列的通项公式；

(2) 对任意正整数，若，求证：；

（3）设,求证：.

正确答案

知识点

裂项相消法求和

题型：简答题

简答题 · 15 分

已知等差数列的前项和为，且．

18. 求；

19. 设满足，，求．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

(Ⅰ)设等差数列的公差为，由，

，

解得,

考查方向

本题考查了等差数列以及前n项和，考察了等比数列的定义以及性质，考察了等比数列的判定及其证明，考查了推理能力与计算能力，属于中档题

解题思路

根据直接得到进而求出通项

易错点

主要易错于公比q=1的判断，

第(2)小题正确答案及相关解析

正确答案

见解析

解析

(Ⅱ) , 是首项为,公比为的等比数列，

时，

考查方向

本题考查了等差数列以及前n项和，考察了等比数列的定义以及性质，考察了等比数列的判定及其证明，考查了推理能力与计算能力，属于中档题

解题思路

利用等比数列的判定得到数列是等比数列，但是要注意q=1

易错点

主要易错于公比q=1的判断，

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：简答题

简答题 · 12 分

已知等差数列{an}前三项的和为－3，前三项的积为8.

(1)求等差数列{an}的通项公式；

(2)若a2，a3，a1成等比数列，求数列{|an|}的前n项和。

正确答案

(1) an＝－3n＋5或an＝3n－7 ；(2)

解析

(1)设等差数列{|an|}的公差为d，则a2＝a1＋d，a3＝a1＋2d，

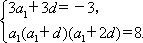
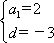
由题意得解得或

所以由等差数列通项公式可得

an＝2－3(n－1)＝－3n＋5或an＝－4＋3(n－1)＝3n－7.

故an＝－3n＋5或an＝3n－7.

(2)当an＝－3n＋5时，a2，a3，a1分别为－1，－4,2，不成等比数列，不满足条件；

当an＝3n－7时，a2，a3，a1分别为－1,2，－4，成等比数列，满足条件。

故|an|＝|3n－7|＝

记数列{|an|}的前n项和为Sn.

当n＝1时，S1＝|a1|＝4；

当n＝2时，S2＝|a1|＋|a2|＝5；

当n≥3时，

Sn＝S2＋|a3|＋|a4|＋…＋|an|＝5＋(3×3－7)＋(3×4－7)＋…＋(3n－7)

＝.

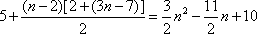
当n＝2时，满足此式。

综上，

知识点

由数列的前几项求通项等差数列的性质及应用等比数列的基本运算等比数列的性质及应用其它方法求和

题型：单选题

单选题 · 5 分

已知数列的前项和为，，，则

正确答案

解析

可知，当时得

当时，有 ① ②

①－②可得即，故该数列是从第二项起以为首项，以为公比的等比数列，故数列通项公式为，

故当时，

当时，，故选答案B

知识点

其它方法求和

题型：单选题

单选题 · 5 分

已知，则等于（　　）

正确答案

解析

相邻两项依次结合可得：

知识点

其它方法求和

题型：简答题

简答题 · 12 分

甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为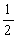，各局比赛的结果相互独立，第1局甲当裁判。

（1）求第4局甲当裁判的概率；

（2）求前4局中乙恰好当1次裁判的概率。

正确答案

见解析。

解析

（1）记A1表示事件“第2局结果为甲胜”，

A2表示事件“第3局甲参加比赛时，结果为甲负”，

A表示事件“第4局甲当裁判”。

则A＝A1·A2.

P(A)＝P(A1·A2)＝P(A1)P(A2)＝.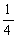

（2）记B1表示事件“第1局比赛结果为乙胜”，

B2表示事件“第2局乙参加比赛时，结果为乙胜”，

B3表示事件“第3局乙参加比赛时，结果为乙胜”，

B表示事件“前4局中乙恰好当1次裁判”。

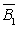
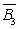
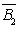
则B＝·B3＋B1·B2·＋B1·.

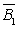
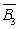
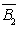
P(B)＝P(·B3＋B1·B2·＋B1·)

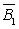
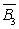
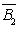
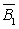
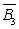
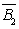
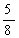
＝P(·B3)＋P(B1·B2·)＋P(B1·)

＝P()P(B3)＋P(B1)P(B2)P()＋P(B1)P()

＝

＝.

知识点

其它方法求和

题型：单选题

单选题 · 5 分

设首项为1，公比为的等比数列{an}的前n项和为Sn，则(　　)。

Asn＝2an－1

Bsn＝3an－2

Csn＝4－3an

Dsn＝3－2an

正确答案

解析

＝3－2an，故选D.

知识点

等比数列的基本运算等比数列的性质及应用其它方法求和

题型：单选题

单选题 · 5 分

6．定义为个正数的“均倒数”，若已知数列的前项的“均倒数”为，又，则（）

正确答案

解析

由“均倒数”为得Sn=5n2，则an=10n-5,=2n-1,

则。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查数列的综合运算

解题思路

（1）求出an；（2）求出bn，利用裂项相消法求和，即可得到结果。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

本题易在求an时发生错误。

知识点

裂项相消法求和

题型：简答题

简答题 · 16 分

19. 设数列的前项和，，，且当时，．

（1）求证:数列是等比数列，并求数列的通项公式；

（2）令，记数列的前项和为．设是整数，问是否存在正整数，使等式成立？若存在，求出和相应的值；若不存在，说明理由．

正确答案

见解析

解析

解：（1）当时, ,,

代入并化简得,

而恒为正值,∴

∴数列是等比数列.

∴.当时,,

又，∴

（2）当时，,此时，又

∴.

故，

当时，

，

若，

则等式为，不是整数，不符合题意；

若，则等式为，

∵是整数, ∴必是的因数, ∵时

∴当且仅当时，是整数，从而是整数符合题意.

综上可知，当时，存在正整数，使等式成立，

当时，不存在正整数使等式成立.

考查方向

本题考查了等比数列的证明及数列的通项公式求法

解题思路

利用，得数列是等比数列.

易错点

忽略n的范围的讨论。

知识点

由an与Sn的关系求通项an等比数列的判断与证明裂项相消法求和数列与函数的综合

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 数列求和、数列的综合应用

扫码查看完整答案与解析