- 数列求和、数列的综合应用
- 共397题
已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数 y=|x2-2x-3| 与 y=f(x) 图像的交点为(x1,y1),(x2,y2),…,(xm,ym),则
正确答案
知识点
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
对于无穷数列{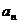
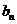
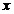
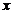
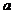


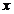
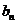
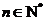
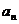
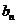
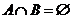
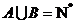
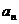
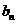
(1)若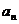
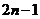
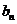
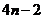
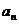
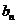
(2)若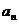
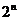
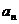
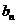
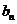
(3)若{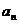
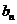
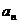
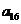
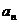
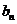
正确答案
(1)因为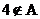
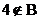

从而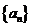
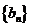
(2)因为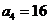
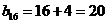
数列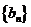
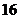
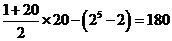
(3)设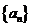
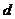
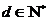
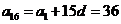
由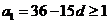
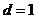
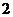
若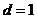
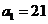
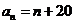
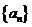
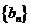
若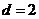
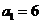
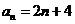
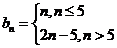
综上,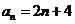
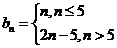
知识点
14.无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意的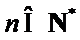
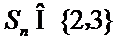
正确答案
解析
由于 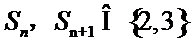
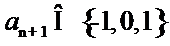
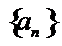
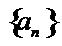
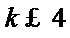
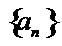
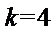
考查方向
解题思路
归纳,推理
易错点
推理的切入点
知识点
12. 已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数 y=|x2-2x-3| 与 y=f(x) 图像的交点为(x1,y1),(x2,y2),…,(xm,ym),则
正确答案
知识点
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
4.已知数列



正确答案
解析
因为











考查方向
解题思路
首先整理关系是





易错点
容易在指数运算、对数运算出错
知识点
4.已知数列



正确答案
解析
因为











考查方向
解题思路
首先整理关系是





易错点
容易在指数运算、对数运算出错
知识点
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
17.在公比为




(Ⅰ)求
(Ⅱ)若函数








正确答案
见解析
解析
试题分析:本题属于数列和三角函数中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意图像的应用.
(Ⅰ) 解:由题可知

故
(Ⅱ)∵点

∴

如图,连接

又∵
∴
∴
∴
考查方向
本题考查了数列与三角函数的知识,涉及到等比数列及三角函数的应用,是高考题中的高频考点.
解题思路
本题考查数列与三角函数的知识,解题步骤如下:利用通项公式求解,利用函数图像性质代入求解。
易错点
三角函数图像易错。
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
扫码查看完整答案与解析





























