- 数列求和、数列的综合应用
- 共397题
21.已知等差数列


(I)求数列

(II)设数列{








正确答案
(I)由已知得





又








(II)由



当n=1时,


当n>1时,



(1)-(2)得 











=1+2




解析
解析已在路上飞奔,马上就到!
知识点
4.在函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知数列{


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2.a4的等差中项。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设递增等差数列






(I)求数列
(II)求数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.数列
(1)求证:数列
(2)求数列
(3)等差数列


正确答案
(1)
又
所以
数列
(2)
(3)
等差数列
设公差为
则
又

解析
解析已在路上飞奔,马上就到!
知识点
6.在正项等比数列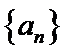
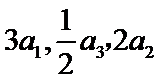
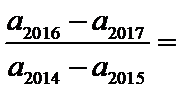
正确答案
解析
由题可知:a3=3a1+2a2,即a1q2=3a1+2a1q,解得q=-1(舍去)或q=2.a2016=a2014q2,
a2017=a2014q3,a2015=a2014q,约分即可。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1、求出q;
2、代入计算,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在求q时发生错误。
知识点
设等比数列




18.求数列
19.设



正确答案
数列



解析
解:
即

考查方向
解题思路
利用数列的性质,建立方程,求出通项公式,在求和时进行分类。
易错点
求和时绝对值的分类讨论。
正确答案
数列



解析
解:



当
两式相减,得
考查方向
解题思路
利用数列的性质,建立方程,求出通项公式,在求和时进行分类。
易错点
求和时绝对值的分类讨论。
5. 已知数列


正确答案
解析
通过观察,可以看到,b2,b16和b9之间的关系,可以得到

考查方向
解题思路
利用等差中项求b9,进而求解答案
易错点
发现不到b2b16和b9之间的关系。
知识点
17.在公比为




(Ⅰ)求
(Ⅱ)若函数








正确答案
见解析
解析
试题分析:本题属于数列和三角函数中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意图像的应用.
(Ⅰ) 解:由题可知

故
(Ⅱ)∵点

∴

如图,连接

又∵
∴
∴
∴
考查方向
本题考查了数列与三角函数的知识,涉及到等比数列及三角函数的应用,是高考题中的高频考点.
解题思路
本题考查数列与三角函数的知识,解题步骤如下:利用通项公式求解,利用函数图像性质代入求解。
易错点
三角函数图像易错。
知识点
扫码查看完整答案与解析
































































