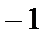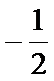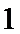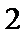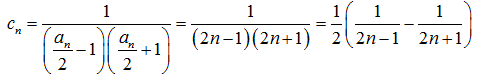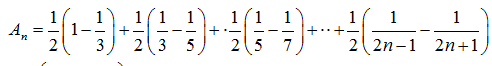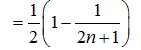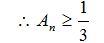- 数列求和、数列的综合应用
- 共397题
19.
已知数列{an}的首项为1, Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q﹥0,n∈N+
(Ⅰ)若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;
(Ⅱ)设双曲线x2﹣=1的离心率为en,且e2=2,求e12+ e22+…+en2,
正确答案
知识点
已知数列{an}的首项为1, Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q﹥0,n∈N+
(Ⅰ)若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;
(Ⅱ)设双曲线x2﹣=1的离心率为en,且e2=2,求e12+ e22+…+en2,
正确答案
(本小题满分12分)
(Ⅰ)由已知,

又由



所以,数列
从而
由



所以
(Ⅱ)由(Ⅰ)可知,
所以双曲线

由


知识点
21.设数列






(Ⅰ) 求数列
(Ⅱ)是否存在实数


正确答案
(Ⅰ)由题意可得:



①─②得



(Ⅱ)解法一:
若
则
得
又


故存在实数

解法二:
欲使


故存在实数

解析
解析已在路上飞奔,马上就到!
知识点
21.已知各项均为正数的数列


(1)求数列
(2)若



正确答案
(1)由已知 
当

①-② 得
整理得
又n=1时 


故
(2)由
得
则
=
=

①-②,得
=
解得
解析
解析已在路上飞奔,马上就到!
知识点
4.在函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列



(1)求数列
(2)若函数

(3)设







正确答案
相加得:
所以
解析
解析已在路上飞奔,马上就到!
知识点
15.设A和B是抛物线上的两个动点,且在A和B处的抛物线切线相互垂直, 已知由










则
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
18.设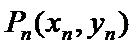
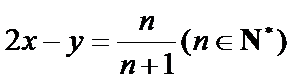
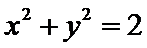
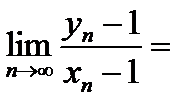
正确答案
解析
当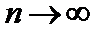
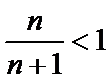
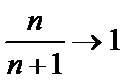
而由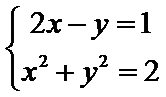
所以
而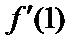
又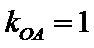
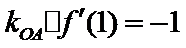
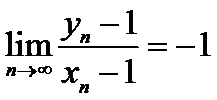
故选A.
知识点
18. 已知数列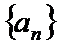
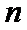
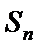
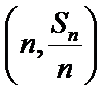
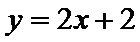
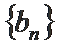
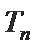
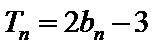
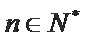
(Ⅰ)求数列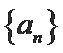
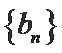
(Ⅱ)设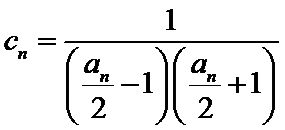
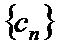
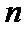
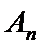
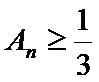
正确答案
(1)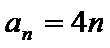
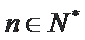
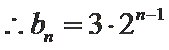
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 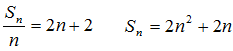
当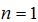
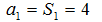
当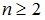
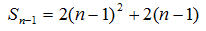
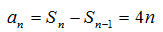
综上,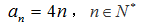
又
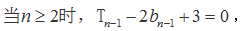
数列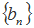
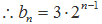
(Ⅱ)
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
已知数列






正确答案

解析
略
知识点
扫码查看完整答案与解析