- 抛物线的标准方程和几何性质
- 共169题
12. 直线




正确答案
解析
设切点B的横坐标为










考查方向
本题考查了导数的几何意义,在近几年的各省高考题出现的频率较高.
解题思路
设出切点,根据切点与斜率求出直线方程.
易错点
如果由点A与斜率确定直线方程,则该题不易算出.
知识点
15.已知P是抛物线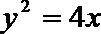
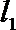
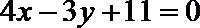
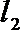
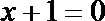
正确答案
3
解析
过点P作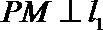
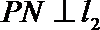
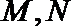
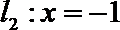
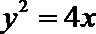
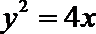
由抛物线的定义,得|PN|=|PF|,过点P作直线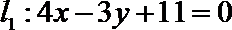
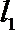
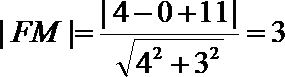
所以P到直线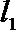
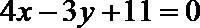
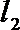
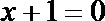
考查方向
本题主要考查了抛物线的定义和标准方程。
易错点
本题易在得到|PN|=|PF|时出现错误,易忽视“利用抛物线的定义将抛物线上的点到准线的距离转化为到焦点的距离”的应用.
知识点
6.抛物线





正确答案
解析
因为抛物线











考查方向
本题主要考查了抛物线的定义的应用。
易错点
本题易在将抛物线上的点到直线

知识点
13.已知双曲线

正确答案
解析
本题考查抛物线的焦点坐标,双曲线的离心率、焦点坐标、渐近线方程等知识。
解:因为抛物线为



考查方向
本题主要考查了抛物线的焦点坐标,双曲线的离心率、焦点坐标、渐近线方程等知识,在各地的高考题中出现的频率较高,属于中档题,考查学生对基础知识的掌握与分析问题的能力。
易错点
双曲线中c2=a2+b2,易与椭圆中a2=b2+c2 搞混.
知识点
7.已知双曲线

正确答案
解析
易知,抛物线焦点坐标为




考查方向
本题主要考查了求双曲线的标准方程,在近几年的各省高考题出现的频率较高,常与椭圆、抛物线等知识点交汇命题。
解题思路
先求出抛物线的焦点坐标,即求出此b,再根据c2=a2+b2即可求出双曲线的标准方程。
易错点
抛物线与双曲线定义不清楚导致出错。
知识点
扫码查看完整答案与解析






