- 由数列的前几项求通项
- 共480题
16. 在数列{an}中,a1=

(1)求an,Sn;
(2)设bn=log2(2Sn+1)﹣2,数列{cn}满足cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,数列{cn}的前n项和为Tn,求使4Tn>2n+1﹣
正确答案
见解析。
解析
(1)由Sn=an+1﹣

两式作差得:an=an+1﹣an,即2an=an+1(n≥2),
∴
又
∴
∴数列{an}是首项为
则

(2)bn=log2(2Sn+1)﹣2=
∴cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,
即


=


由4Tn>2n+1﹣

即
∴使4Tn>2n+1﹣
知识点
17.数列{an}中,a1=

(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值。
正确答案
见解析。
解析
(1)由Sn+1﹣Sn=(

又

从而
(2)由(Ⅰ)可得


从而由S1,t(S1+S2),3(S2+S3)成等差数列可得:
知识点
12.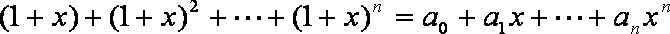
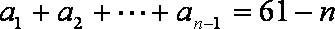
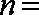
正确答案
5
解析
显然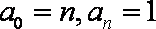
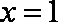
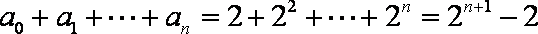
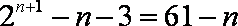
知识点
22.已知数列



(1)求数列


(2)数列





(3)设


正确答案
(1)
(2)
(3)3
解析
(1) 



∴令

∴数列


∴
(2) 由



故
当

于是,
当

当
又

综上,有
(3)

∴

∴数列



知识点
9.若

正确答案
解析

知识点
扫码查看完整答案与解析