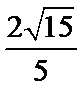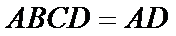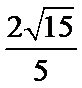- 空间两点间的距离公式
- 共8题
19.如图4所示,在矩形









(Ⅰ)求证:平面

(Ⅱ)若四棱锥


正确答案
(1)略;(2)
解析
.证明:(Ⅰ)∵


∴

故在四棱锥
又∵


∴

又



(Ⅱ)设


在等腰直角


由(Ⅰ)知

故
整理得

连结


于是
∵ 

设点F到



由
所以点F到平面

考查方向
解题思路
第(1)问先根据等腰证明


第(2)问先证明


易错点
无法找到线面垂直的条件;找不到

知识点
如图,四棱锥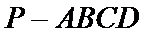
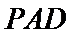
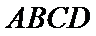
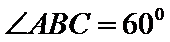
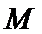
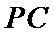
22.求证: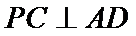
23.求点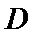
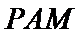
正确答案
(1)略;
解析
(1):取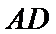
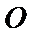
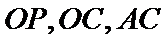
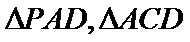
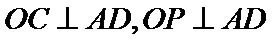
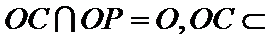
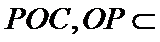
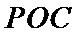
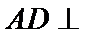
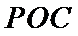
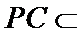
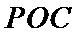
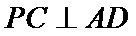
考查方向
解题思路
先证明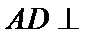
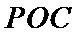
易错点
不会做辅助线导致没有思路;
正确答案
(2)
解析
(2)点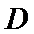
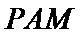
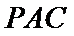
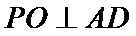
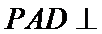
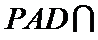

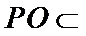
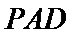
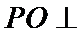
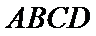
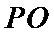
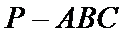
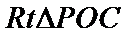
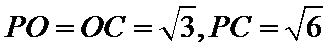
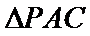
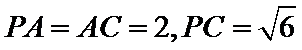
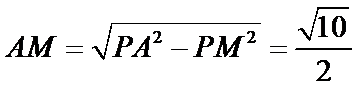
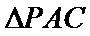
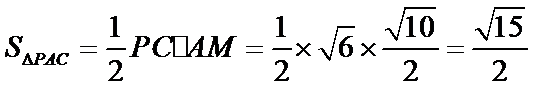
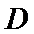
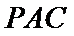
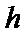
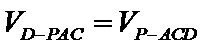
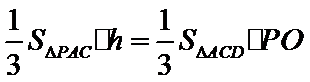
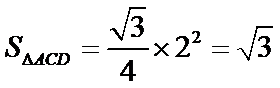
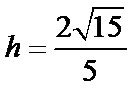
考查方向
解题思路
先发现点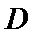
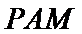
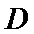
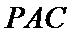
易错点
看不出点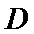
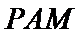
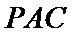
如图,在三棱柱




22.求证:

23.当三棱锥


正确答案
(略)
解析
连结















考查方向
解题思路
关键是在面DCB1中找线,连结


易错点
确定“三棱锥
正确答案
解析
设点








由(Ⅰ)知:




∵




∵




















考查方向
解题思路
当三棱锥





易错点
确定“三棱锥
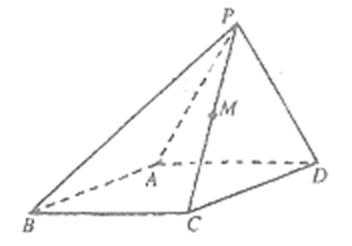
18.如图





(1)证明:

(2)证明:
(3)求点

正确答案
(1)由四边形



(2)先证



(3)取












试题解析:
(1)因为四边形






(2)因为四边形











(3)取































解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析