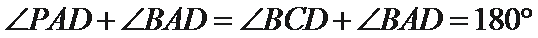二元二次方程表示圆的条件
共62题

二元二次方程表示圆的条件
共62题

热门试卷

题型：简答题

简答题 · 14 分

20.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

有一块正方形菜地EFGH，EH所在直线是一条小河，收获的蔬菜可送到F点或河边运走.于是，菜地分为两个区域S1和S2，其中S1中的蔬菜运到河边较近，S2中的蔬菜运到F点较近，而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等.现建立平面直角坐标系，其中原点O为EF的中点，点F的坐标为（1，0），如图

（1）求菜地内的分界线C的方程；

（2）菜农从蔬菜运量估计出S1面积是S2面积的两倍，由此得到S1面积的“经验值”为 .设M是C上纵坐标为1的点，请计算以EH为一边、另有一边过点M的矩形的面积，及五边形EOMGH的面积，并判别哪一个更接近于S1面积的“经验值”.

正确答案

20.解：（1）因为C上的点到直线EH与到点F的距离相等，所以C是以F为焦点、以

EH为准线的抛物线在正方形EFGH内的部分，其方程为．

（2）依题意，点M的坐标为

所求的矩形面积为，而所求的五边形面积为．

矩形面积与“经验值”之差的绝对值为，而五边形面积与“经验值”之差

的绝对值为，所以五边形面积更接近于S1面积的“经验值”．

知识点

二元二次方程表示圆的条件

题型：单选题

单选题 · 5 分

圆（x+1）2+y2=2的圆心到直线y=x+3的距离为

正确答案

知识点

二元二次方程表示圆的条件

题型：填空题

填空题 · 5 分

13.如图，AB是圆的直径，弦CD与AB相交于点E，BE=2AE=2，BD=ED，则线段CE的长为__________.

正确答案

知识点

二元二次方程表示圆的条件

题型：简答题

简答题 · 10 分

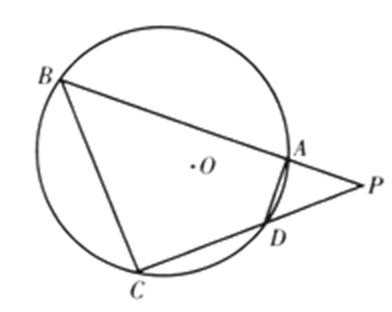
22．选修4-1：几何证明选讲

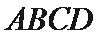
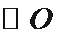
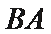
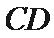
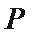
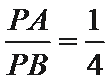
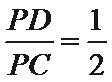
如图，四边形是的内接四边形，延长和相交于点，，．

（1）求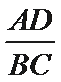的值；

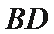
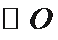
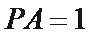
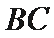
（2）若为的直径，且，求的长．

正确答案

（1）

（2）．

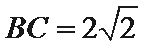
解析

试题分析：本题属于几何证明选讲中的基本问题，题目的难度一般，解题过程如下：

（1）∵

∴，，得与相似．

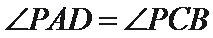
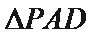
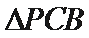
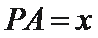
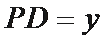
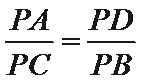
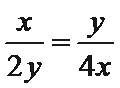
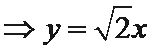
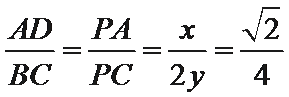
设，，则有，．

∴．

（2）由题意知，，，∴． ∴．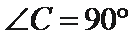

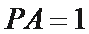
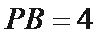
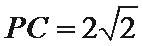
∴在中，，∴．

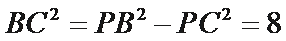
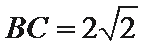
考查方向

本题考查了几何证明选讲的专题知识，考查了相似性的问题。

解题思路

本题考查几何证明选讲的相关知识，主要考查了相似性的问题，通过三角形相似即可求解。

易错点

对几何定理记忆不熟练，看不出图中的几何关系而导致做错。

知识点

二元二次方程表示圆的条件

题型：简答题

简答题 · 12 分

如图椭圆的离心率为，其左顶点在圆上.

24.求椭圆的方程；

25.直线与椭圆的另一个交点为，与圆的另一个交点为.

（i）当时，求直线的斜率；

（ii）是否存在直线，使得? 若存在，求出直线的斜率；若不存在，说明理由.

第(1)小题正确答案及相关解析

正确答案

解析

试题分析：本题属于圆锥曲线的问题，（1）考查求椭圆的标准方程，（2）1.弦长公式，2.利用反正法最后推出矛盾。

考查方向

本题考查了椭圆的方程及直线和椭圆的位置关系。

解题思路

（1）由已知条件很容易求出椭圆的方程，

（2）1.利用弦长公式即可解出，

2，利用反证法思想求解。

易错点

第2问不知道用设而不求的方法来解答且相对计算量点大。

第(2)小题正确答案及相关解析

正确答案

1.，

2.不存在．

解析

试题分析：本题属于圆锥曲线的问题，（1）考查求椭圆的标准方程，（2）1.弦长公式，2.利用反正法最后推出矛盾。

（i）设点，显然直线存在斜率，

设直线的方程为，与椭圆方程联立得,

化简得到，

因为为上面方程的一个根，所以，

所以由，

代入得到，解得, 所以直线的斜率为.

（ii）圆心到直线的距离为， .

因为，

代入得到.

显然，所以不存在直线，使得.

考查方向

本题考查了椭圆的方程及直线和椭圆的位置关系。

解题思路

（1）由已知条件很容易求出椭圆的方程，

（2）1.利用弦长公式即可解出，2，利用反证法思想求解。

易错点

第2问不知道用设而不求的方法来解答且相对计算量点大。

继续学习学习下一知识点

下一知识点 : 点与圆的位置关系

百度题库 > 高考 > 文科数学 > 二元二次方程表示圆的条件

扫码查看完整答案与解析