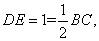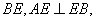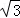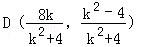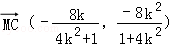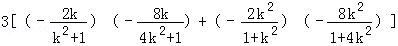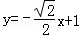- 平面与平面垂直的判定与性质
- 共129题
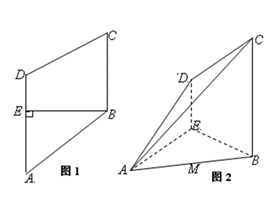
如图1,在梯形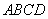
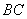
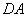
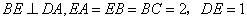
将四边形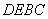
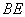
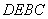
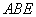
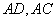
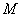
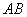
(1)若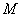
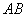
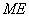
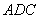
(2)若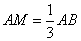
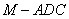
正确答案
见解析。
解析
(1)取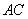
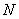
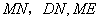
∵ 
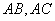
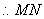
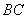
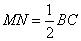
又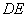
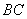
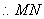
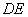
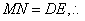
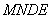
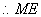
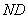
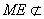
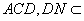
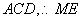
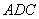
(2)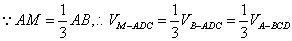

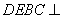
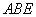
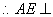
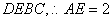
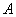
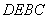
又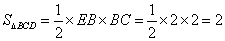
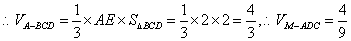
知识点
把三阶行列式



正确答案
解析
略
知识点
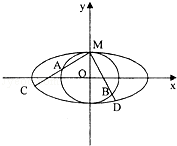
如图,圆O与离心率为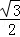
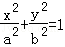
(1)求椭圆T与圆O的方程;
(2)过点M引两条互相垂直的两直线l1、l2与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为d1、d2,求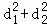
②若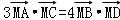
正确答案
见解析。
解析
(1)由题意知: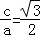
又a2=b2+c2,所以a2=c2+1,
联立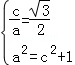
所以椭圆C的方程为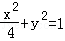
(2)①设P(x0,y0)因为l1⊥l2,则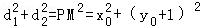
因为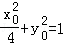
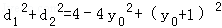
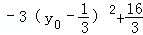
因为﹣1≤y0≤1,所以当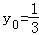
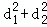
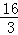
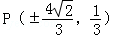
②设l1的方程为y=kx+1,
由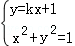
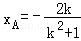
代入y=kx+1得: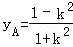
所以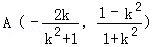
由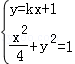
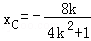
代入y=kx+1得: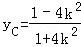
所以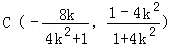
把A,C中的k置换成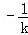
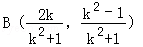
所以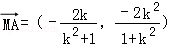
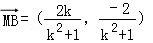
由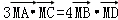
得
=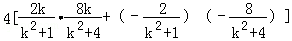
整理得: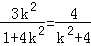
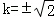
所以l1的方程为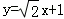
或l1的方程为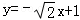
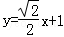
知识点
如图,在四棱锥












(1)若



(2)求证:平面

(3)是否存在点


写出证明过程并求出线段
正确答案
见解析
解析
(1)因为

所以 
因为

而



所以

(2)因为平面

平面




所以




又因为



而

所以平面

(3)存在点


在棱


由已知,



由平面几何知识可得 
由(2)知,


因为


而


又因为


在

可求得,
可见直线



知识点
已知复数

正确答案
2
解析
略
知识点
扫码查看完整答案与解析