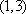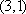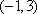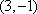- 复数
- 共721题
3.设复数z满足z2=3+4i(i是虚数单位),则z的模为 .
正确答案
解析
复数z满足z2=3+4i,可得|z||z|=|3+4i|=

故答案为:
考查方向
解题思路
直接利用复数的模的求解法则,化简求解即可.
易错点
本题考查复数的模的求法,注意复数的模的运算法则的应用,考查计算能力
知识点
2.设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )
正确答案
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在复平面内,复数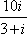
正确答案
解析
考查的是复数除法的化简运算以及复平面,实部虚部的概念。
因为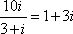
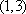
知识点
复数z=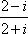

正确答案
解析
因为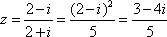
知识点
14.已知复数z=m﹣i(m∈R,i为虚数单位),若(1+i)z为纯虚数,则|z|= .
正确答案
解析
因为(1+i)z为纯虚数,即(1+i)(m-i)=m+1-(m-1)i为复数,则m+1=0且m-1≠0,则m=-1,则z=-1-i,则|z|=
考查方向
复数的计算,纯虚数的概念,复数的模的计算
解题思路
先计算出z,然后求z的模
易错点
纯虚数的概念和复数的模
教师点评
本题主要考查复数的计算,难度一般。但需要掌握纯虚数的概念。
知识点
1.复数
正确答案
解析
分子分母同时乘以1-i,得到1-i,对应的点为(1,-1),对应的在复平面内的第四象限。
解题思路
本题考查复数的运算,及复平面内点的坐标问题
易错点
在进行复数运算时,正负号容易出错,分子分母必须同时乘以1-i,将分母进行转化。
知识点
10.已知



正确答案
解析
考查方向
复数的概念与运算
解题思路
教师点评
知识点
1.复数
正确答案
解析
见解题思路。
考查方向
复数的运算和相关概念。
解题思路


易错点
易错选D。
教师点评
注意:复数的实部和虚部均为实数。
知识点
扫码查看完整答案与解析