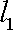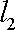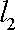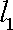函数单调性的性质
共384题

· 函数单调性的性质

函数单调性的性质
共384题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设α、β是两个不同的平面，m、n是平面α内的两条不同直线，l1,l2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是 ( )

Am∥且n∥

Bm∥β且n∥

Cm∥β且n∥β

Dm∥β且∥α

正确答案

解析

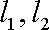
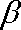
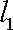
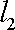
因为是平面内的两条相交直线，且m∥且n∥，所以根据面面平行的判定定理可知α∥β，反之未必成立，答案选A.

知识点

函数单调性的性质

题型：简答题

简答题 · 16 分

已知数列.如果数列满足，

，其中，则称为的“生成数列”。

（1）若数列的“生成数列”是，求；

（2）若为偶数，且的“生成数列”是，证明：的“生成数列”是；

（3）若为奇数，且的“生成数列”是，的“生成数列”是，….依次将数列

，，，…的第项取出，构成数列.

证明：是等差数列。

正确答案

见解析

解析

（1）解：由题意得：；；

；

（2）因为，，，

…… ，

由于为偶数，将上述个等式中的第这个式子都乘以，相加得

即，.

由于，，

根据“生成数列”的定义知，数列是的“生成数列”.

（3）证法一：

证明：设数列,,中后者是前者的“生成数列”.欲证成等差数列，只需证明成等差数列，即只要证明即可.

由（2）中结论可知，

，

所以，，即成等差数列，

所以是等差数列.

证法二：

因为，

所以 .

所以欲证成等差数列，只需证明成等差数列即可.

对于数列及其“生成数列”，

因为，，，

…… ，

由于为奇数，将上述个等式中的第这个式子都乘以，

相加得

即.

设数列的“生成数列”为，因为，，

所以，即成等差数列。

同理可证，也成等差数列。即是等差数列。

所以成等差数列.

知识点

函数单调性的性质

题型：单选题

单选题 · 5 分

若、为实数，则“＜1”是“0＜＜”的

A充分而不必要条件

B必要而不充分条件

C充分条件

D既不充分也不必要条件

正确答案

解析

，所以，所以“” 是“”的必要而不充分条件，选B.

知识点

函数单调性的性质

题型：单选题

单选题 · 5 分

执行如图所示的程序框图，输出的S值为

B—6

C10

D-15

正确答案

解析

第一次循环为：，第二次循环为：，第三次循环为：，第四次循环为：，第五次循环条件不成立，输出,答案选C.

知识点

函数单调性的性质

题型：简答题

简答题 · 14 分

如图四棱锥中，底面是平行四边形，，平面，，，是的中点.

（1）求证：平面；

（2）试在线段上确定一点，使∥平面，并求三棱锥-的体积.

正确答案

见解析

解析

解：（1）证明：四边形是平行四边形，，

平面，又，，平面.

（2）设的中点为，在平面内作于，则平行且等于，连接，则四边形为平行四边形，

∥，平面，平面，

∥平面，为中点时，∥平面.

设为的中点，连结，则平行且等于，

平面，平面，

知识点

函数单调性的性质

继续学习学习下一知识点

下一知识点 : 复合函数的单调性

百度题库 > 高考 > 文科数学 > 函数单调性的性质

扫码查看完整答案与解析