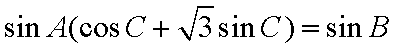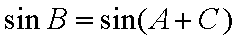- 函数单调性的性质
- 共384题
某大学体育学院在2012年新招的大一学生中,随机抽取了40名男生, 他们的身高(单位:cm)情况共分成五组:第1组[175,180),第 2 组[180,185),第 3 组 [185,190),第 4 组[190,195),第 5 组[195,200) .得到的频率分布直方图(局部)如图所 示,同时规定身高在185cm以上(含185cm)的学生成为组建该校篮球队的“预备生”.
(1)求第四组的频率,并补全该频率分布直方图;
(2)在抽取的40名学生中,用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
正确答案
见解析
解析
解析:(1)其它组的频率和为
(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2…………4分
(2)解法一:依题意“预备生”与“非预备生”的人数比为3:2,所以采用分层抽样的方法抽取的3名“预备生”记为a、b、c,2名“非预备生”为m、n.则基本事件是(a,b),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),(c,n),(m,n)共10个.其中满足至少有1人是“预备生”的基本事件有9个,故所求的概率为P=
解法二:依题意“预备生”与“非预备生”的人数比为3:2,所以采用分层抽样的方法抽取的3名“预备生”记为a、b、c,2名“非预备生”为m、n.则基本事件是(a,b),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),(c,n),(m,n)共10个.其中2名都是“非预备生”的基本事件有1个,故所求的概率为P=1-

知识点
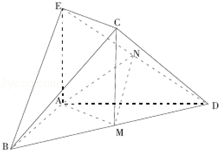
如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABD,M为线段BD的中点,MC∥AE,AE=MC=
(1)求证:平面BCE丄平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC。
正确答案
见解析。
解析
(1)∵AB=AD=2,AB丄AD,M为线段BD的中点,
∴AM=BD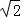
∵AE=MC=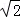
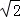
∵AE丄平面ABD,MC∥AE,
∴MC⊥平面ABD,∴平面CBD⊥平面ABD,∴AM⊥平面CDB。
又MC∥AE,AE=MC=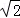
∴EC∥AM,∴EC⊥平面CDB,∴BC⊥EC,∵EC∩CD=C
又∵BC⊥平面CDE,
∴平面BCE⊥平面CDE。
(2)∵BD中点M,ED的中点N,∴MN∥BE,
又∵MN⊄平面BCE,BE⊂平面BCE,
∴MN∥平面BEC
由(1)知EC∥AM,又∵AM⊄平面BCE,EC⊂平面BCE,
∴AM∥平面BEC,且AM∩MN=M。
∴平面AMN∥平面BEC。
知识点
已知函数


(1)求实数
(2)是否存在实数



(3)若

正确答案
见解析
解析
本题主要考查函数、导数、不等式等基本知识;考查运算求解能力、推理论证能力;考查化归转化思想、函数方程的思想、分类整合思想、数形结合思想。
(1) 
依题意可得
解得
(2)

①当




②当



③当








综上所述,存在

(3)解法一:由(2)知,




即







(3)解法二:
设

当







知识点
在ΔABC中,角A,B,C所对的边分别为a,b,c,a(cosC+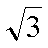
(1)求角A的大小
(2)若a=1,SΔABC=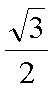
正确答案
见解析
解析
(1)由正弦定理得:
又
化简得: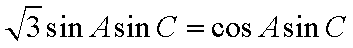
故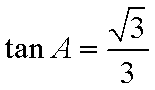
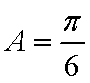
(2)根据题意得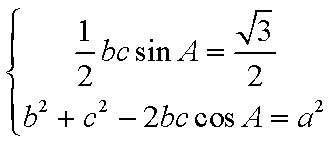
把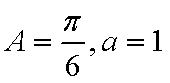
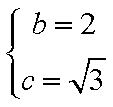
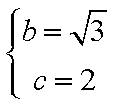
知识点
在等差数列


(1)求
(2) 若





正确答案
见解析
解析
解:
(1) 由题意得:
解得:

(2) 因为


所以


所以当

当

知识点
扫码查看完整答案与解析