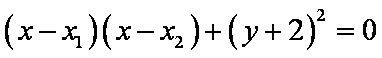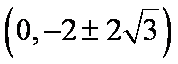- 函数单调性的性质
- 共384题
数列
若存在正整数k,使
正确答案
解析


知识点
已知

正确答案
﹣7
解析
∵

∴
两式相比得
即4sinx+4cosx=3sinx﹣3cosx,
∴sinx=﹣7cosx,
∴tanx=﹣7,
知识点
如图,椭圆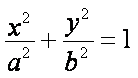
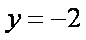
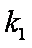
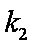
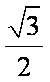
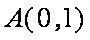
(1)求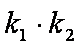
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点,
若过定点,求出该定点,如不过定点,请说明理由。
正确答案
见解析
解析
(1)因为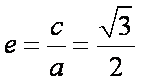
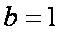
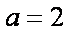
所以椭圆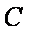
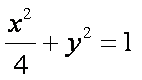
设椭圆上点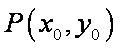
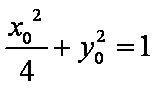
所以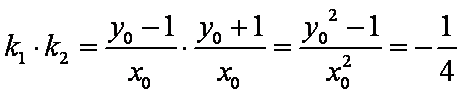
(2)因为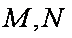
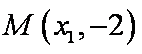
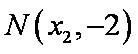
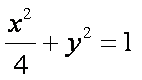
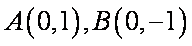
所以
又由(1)知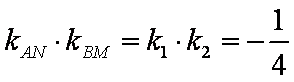
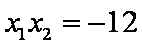
不妨设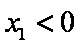
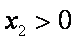

所以当且仅当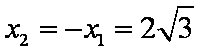
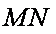
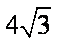
(3)设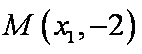
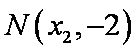
则以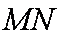
即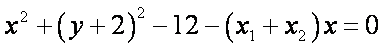
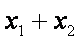
所以有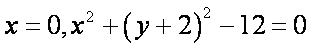
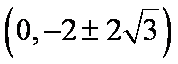
所以,无论点P如何变化,以MN为直径的圆恒过定点
知识点
在直角坐标系xOy中,已知A(﹣1,0),B(0,1),则满足PA2﹣PB2=4且在圆x2+y2=4上的点P的个数为 。
正确答案
2
解析
设P(x,y),
∵A(﹣1,0),B(0,1),
由PA2﹣PB2=4,得(x+1)2+y2﹣x2﹣(y﹣1)2=4。
整理得:x+y=2。
联立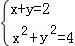
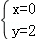
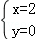
∴P点坐标为(0,2)或(2,0)。
即满足条件的P点的个数为2。
知识点
已知函数
(1)若


(2)若



正确答案
见解析
解析
(1)因为












所以


(2)当


当


当


当




当


当



所以,当


当


当


综上所述,当




所以函数



知识点
扫码查看完整答案与解析