- 两条直线垂直的判定
- 共80题
直线x+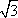
正确答案
解析
圆心O到直线AB的距离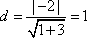
所以
知识点
如图所示,程序框图(算法流程图)的输出结果是 .
正确答案
15
解析
略
知识点
在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A,B两点,则弦AB的长等于( )
正确答案
解析
圆x2+y2=4的圆心为O(0,0),半径为r=2.
所以圆心到直线3x+4y-5=0的距离为
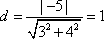
知识点
已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.
正确答案
(1) an=2n. ;(2) (n-1)2n+1+2.
解析
(1)由Sn=kcn-k,
得an=Sn-Sn-1=kcn-kcn-1(n≥2),
由a2=4,a6=8a3,得kc(c-1)=4,kc5(c-1)=8kc2(c-1),
解得
于是an=2n.
(2)
Tn=2+2·22+3·23+4·24+…+n·2n,
Tn=2Tn-Tn=-2-22-23-24-…-2n+n·2n+1=-2n+1+2+n·2n+1=(n-1)2n+1+2.
知识点
已知函数f(x)=ax3+bx+c在点x=2处取得极值c-16.
(1)求a,b的值;
(2)若f(x)有极大值28,求f(x)在[-3,3]上的最小值。
正确答案
(1) a=1,b=-12. ;(2) -4
解析
(1)因f(x)=ax3+bx+c,故f′(x)=3ax2+b,
由于f(x)在点x=2处取得极值c-16,
故有
即
解得a=1,b=-12.
(2)由(1)知f(x)=x3-12x+c;
f′(x)=3x2-12=3(x-2)(x+2)。
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,故f(x)在(-∞,-2)上为增函数;
当x∈(-2,2)时,f′(x)<0,故f(x)在(-2,2)上为减函数;
当x∈(2,+∞)时,f′(x)>0,故f(x)在(2,+∞)上为增函数。
由此可知f(x)在x1=-2处取得极大值f(-2)=16+c,f(x)在x2=2处取得极小值f(2)=c-16.
由题设条件知16+c=28得c=12.
此时f(-3)=9+c=21,f(3)=-9+c=3,f(2)=-16+c=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4
知识点
扫码查看完整答案与解析