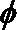两条直线垂直的判定
共80题

· 两条直线垂直的判定

两条直线垂直的判定
共80题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

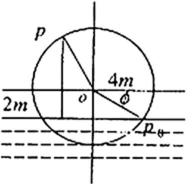
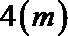
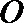
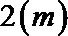
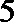
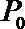
20．如图，一个水轮的半径为，水轮圆心距离水面，已知水轮每分钟转动圈，如果当水轮上点从水中浮现时（图中点）开始计算时间。

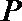
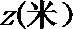
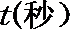
（1）将点距离水面的高度表示为时间的函数，求其解析式；

（2）求点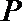第一次到达最高点时所需要的时间。

正确答案

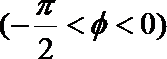
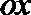
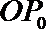
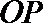
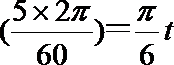
（1）如图建立直角坐标系，设角是以为始边，为终边的角，每分钟内所转过的角为，

得，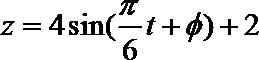

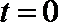
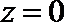
当时，，

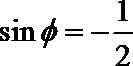
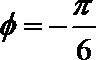
得，即，

故所求的函数关系式为）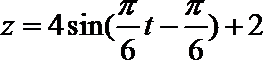

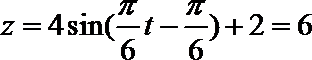
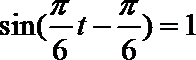
（2）令，得，

取，得，故点第一次到达最高点大约需要秒

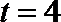
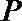
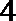
解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：填空题

填空题 · 5 分

已知f（1，1）=1，f（m，n）∈N*（m、n∈N*），且对任意m、n∈N*都有：

① f（m，n+1）= f（m，n）+2； ② f（m＋1，1）=2 f（m，1）。

给出以下三个结论：（1）f（1，5）=9；（2）f（5，1）=16；（3）f（5，6）=26。

其中正确的个数为。

正确答案

解析

略。

知识点

两条直线垂直的判定

题型：填空题

填空题 · 4 分

若三阶行列式中第1行第2列的元素3的代数余子式的值是，则（其中是虚数单位，）的值是。

正确答案

解析

略

知识点

两条直线垂直的判定

题型：单选题

单选题 · 5 分

是直线垂直的（）

A充分而不必要条件

B必要而不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

略

知识点

充要条件的判定两条直线垂直的判定

题型：填空题

填空题 · 4 分

在的二项展开式中，按的降幂排列，只有第项的系数最大，则各项的二项式系数之和为________（答案用数值表示）。

正确答案

256

解析

略

知识点

两条直线垂直的判定

题型：简答题

简答题 · 12 分

已知抛物线的准线为，焦点为F，的圆心在轴的正半轴上，且与轴相切，过原点O作倾斜角为的直线，交于点A，交于另一点B，且AO=OB=2.

（1）求和抛物线C的方程；

（2）过上的动点Q向作切线，切点为S，T，求证：直线ST恒过一个定点，并求该定点的坐标。

正确答案

见解析。

解析

知识点

两条直线垂直的判定

题型：填空题

填空题 · 4 分

已知双曲线的左右焦点分别是，设P是双曲线右支上一点，在上的投影的大小恰好为，且它们的夹角为，则双曲线的渐近线方程为

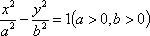
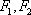
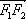
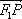
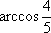
正确答案

解析

略

知识点

两条直线垂直的判定

题型：单选题

单选题 · 5 分

是虚数单位，若，则等于（）

正确答案

解析

，选C

知识点

两条直线垂直的判定

题型：单选题

单选题 · 5 分

已知向量，，且，则的值为（）

正确答案

解析

。

故选B。

知识点

两条直线垂直的判定

题型：单选题

单选题 · 5 分

函数在处切线的斜率为（）

正确答案

解析

略

知识点

两条直线垂直的判定

继续学习学习下一知识点

下一知识点 : 两条直线垂直与倾斜角、斜率的关系

百度题库 > 高考 > 文科数学 > 两条直线垂直的判定

扫码查看完整答案与解析