- 两条直线垂直的判定
- 共80题
如图,矩形




(1)求证:平面

(2)若

正确答案
见解析
解析
(1)因为







因为


又






又





(2)因为

因为
且
所以


因为

因为

知识点
如图,











(1)证明:平面

(2)当三棱锥

正确答案
见解析。
解析
(1)因为






















(2)依题意,
由(1)知



此时,




知识点
已知数列






(1)求数列
(2)若


正确答案
见解析。
解析
(1)由



(2)数列


从而
∴
∴
=
从而.
知识点
如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,则当底面ABC水平放置时,液面的高为 。
正确答案
6
解析
不妨令此三棱柱为直三棱柱,如图
当侧面AA1B1B水平放置时,水的形状为四棱柱形,底面是梯形。
设△ABC的面积为S,则S梯形ABFE=
V水=
当底面ABC水平放置时,水的形状为三棱柱形,设水面高为h,则有V水=Sh,
∴6S=Sh,∴h=6。
故当底面ABC水平放置时,液面高为6。
知识点
如图四棱锥








(1)求证:

(2)试在线段





正确答案
见解析
解析
(1)证明:







(2)设




















设









知识点
设函数
(1)若函数
(2)当a>0时,求
正确答案
见解析。
解析
(1)
①
②当

(2)①当
②当
知识点
如图,在四面体ABCD中,
的中点,点F在线段AC上,且
(1)若EF∥平面ABD,求实数
(2)求证:平面BCD⊥平面AED。
正确答案
见解析。
解析
(1)因为EF∥平面ABD,易得
平面ABC

所以
又点E是BC的中点,点F在线段AC上,
所以点F为AC的中点,
由

(2)因为
所以

又

所以
而
所以平面BCD⊥平面AED。
知识点
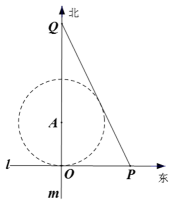
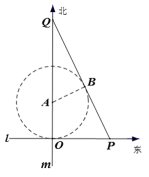
如图,某市有一条东西走向的公路
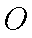
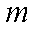
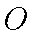
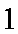
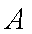
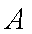
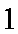
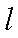
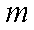
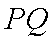
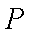
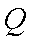
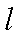
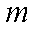
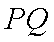
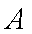
(1)当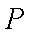
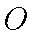
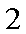
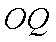
(2)当公路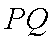
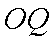
正确答案
见解析。
解析
以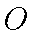
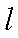
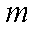
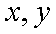
设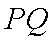
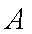
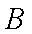
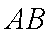
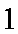
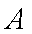
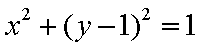
(1)由题意可设直线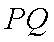
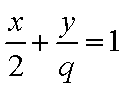
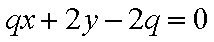
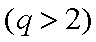
∵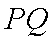
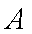
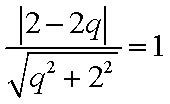
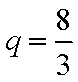
故当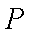
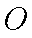
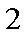
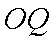
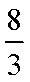
(2)设直线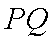
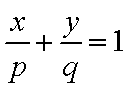
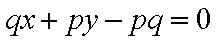
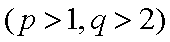
∵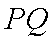
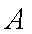
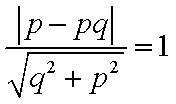
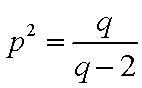
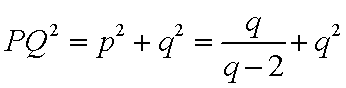
令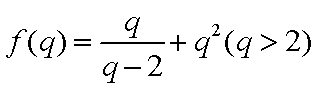
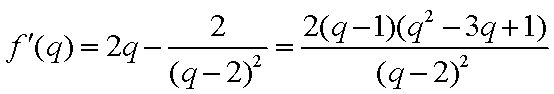
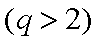
当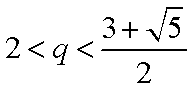
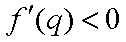
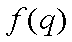
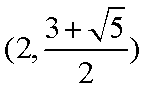
当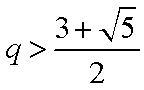
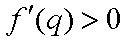
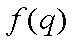
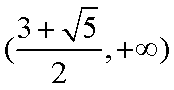
∴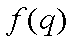
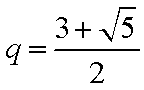
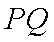
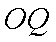
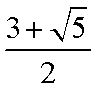
答:(1)当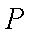
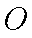
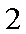
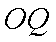
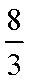
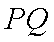
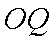
长为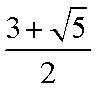
知识点
19.椭圆以坐标轴为对称轴,且经过点



(1)求圆心在线段
(2)在椭圆位于第一象限的弧


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. “


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析