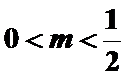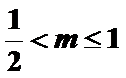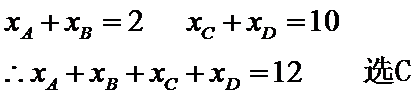- 二次函数的零点问题
- 共21题
14.若函数
正确答案
(-2,+∞)
考查方向
易错点
1.不注意指数函数的有界性导致出错;
知识点
7.已知函数


①

②当


③当

④
其中正确的是( )
正确答案
解析
由图像可知函数的值域为











考查方向
解题思路
先画出函数
易错点
不能准确画出函数的图像导致本题出错。
知识点
12.若函数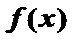


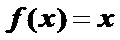
上,

正确答案
解析
当




考查方向
解题思路
根据已知定义域上的解析式求出未知的定义域上的解析式,在结合函数的图像找到要求解的范围。
易错点
本题不会由已知的解析式来求未知定义域上的解析式。
知识点
13.函数
正确答案
解析
函数





考查方向
解题思路
画出图像转化为求图像交点的个数的问题。
易错点
不会用数形结合法做。
知识点
8.已知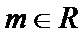
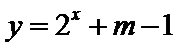
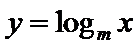
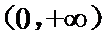
正确答案
解析
若函数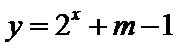
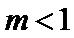
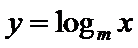
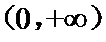
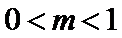
考查方向
解题思路
分别算出使得成立的m的取值范围。
易错点
充分和必要条件的判定出错。
知识点
12.若函数



正确答案
解析
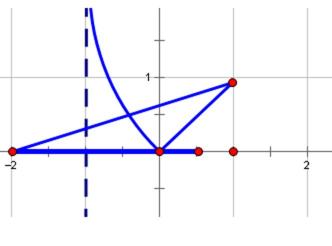
求出函数在(-1,0)的解析式,然后根据f(x)=m(x+2),使得y=f(x)与y=m(x+2)有两个交点,而直线过定点(-2,0),要求的m的范围转化为直线的斜率的取值使得两个函数的图像有2个交点,所以实数m的取值范围是0<m≤
考查方向
解题思路
由已知条件算出对称定义域上的函数解析式,然后转化为两个函数有2个交点的问题来求解。
易错点
不会求对称的定义域上的函数的解析式。
知识点
12.如图,偶函数






正确答案
解析
由图象可知f(x)=0有三个根,0,
由图象可知,g(x)所对的每一个值都能有3个根,因此m=9,同理可得,n=9,所以选A.
考查方向
解题思路
结合函数图象把方程根的个数转化为函数图象的交点
个数,可分别求出m.n,进而得到答案
易错点
数型结合思想的相互转化错误
知识点
10.已知定义在R上的奇函数y=f(x)
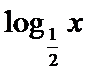
正确答案
解析
根据性质做出图像
共有4个零点ABCD,且AB关于x=1对称
CD关于x=5对称
考查方向
解题思路
1)根据函数性质得出函数在(0,6)上的图像,
2)数形结合得到零点
3)根据对称性得出零点间关系
易错点
主要易错于函数图像不能有效的画出
知识点
7.设函数f(x)=
正确答案
3
解析
由f(-4)=f(0),得16-4b+c=c
且由对称性可知,f(x)在x=-2处取得最小值
即f(-2)=-2,得4-2b+c=-2.
联立方程解得b=4,c=2
所以f(x)=
知识点
12.已知函数f(x)=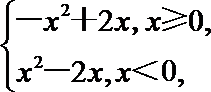
正确答案
解析
设f(x)=t,方程 t2+at-b2=0的两根分别为t1、t2,则t1t2=-b2≤0.若b≠0,则t1、t2异号,由函数图像可知,对应的x值不唯一,因此,b=0。即不等式的解为-a<t<0.注意到t=0时x=0,或x=2.因此a的最大值为8。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查分段函数和不等式
解题思路
1、画出f(x)的图像;
2、利用方程只有一个整数解求解,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在处理只有一个整数解时发生错误。
知识点
扫码查看完整答案与解析