- 直线与圆锥曲线的综合问题
- 共150题
已知













(1)证明:点

(2)设点






正确答案
见解析。
解析
(1)




设
则
由题意得
所以点

经验证点




(2)由




设





由①、②得







故 
又 

所以 
由此知





(2)法二:
同理
所以
因此A、P、B、Q四点在同一圆上。
知识点
已知






(1)求圆
(2)设过点





正确答案
(1) 
(2)
解析
(1)先求圆C关于直线x + y – 2 = 0对称的圆D,由题知圆D的直径为


(2)由(Ⅰ)知
圆C:


由椭圆的焦半径公式得:

所以当
知识点
如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2:
(1)当t为何值时,矩形ABCD的面积取得最大值?并求出其最大面积;
(2)求直线AA1与直线A2B交点M的轨迹方程。
正确答案
(1) 

解析
(1)设A(x0,y0),则矩形ABCD的面积S=4|x0||y0|。
由

x02y02=x02(1-

当


(2)由A(x0,y0),B(x0,-y0),A1(-3,0),A2(3,0)知
直线AA1的方程为
y=
直线A2B的方程为
y=
由①②得
y2=
又点A(x0,y0)在椭圆C上,故
y02=1-
将④代入③得
因此点M的轨迹方程为
知识点
设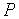
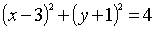
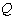
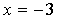
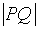
正确答案
解析
∵由圆(x-3)2+(y+1)2=4知,圆心的坐标为(3,-1),半径r=2,
∴圆心到直线x=-3的距离d=|3-(-3)|=6.
∴|PQ|min=d-r=6-2=4,故选B。
知识点
椭圆






正确答案
解析
本题考查的是圆锥曲线的离心率,由题意可知,




知识点
扫码查看完整答案与解析

















