直线与圆锥曲线的综合问题
共150题

· 直线与圆锥曲线的综合问题

直线与圆锥曲线的综合问题
共150题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

10．双曲线（a＞0，b＞0）的左、右焦点分别是F1、F2，过F1作倾斜角为30°的直线交双曲线右支于M点，若MF2⊥x轴，则双曲线的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

21．设椭圆（a＞b＞0）的焦点分别为F1（－1，0），F2（1，0），直线l：x＝交x轴于点A，且＝2．

（Ⅰ）试求椭圆的方程；

（Ⅱ）过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点（如图所示），若四边形DMEN的面积为，求DE的直线方程．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程椭圆的定义及标准方程直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

21.如图，在一点为圆心，为直径的半圆中，为半圆弧的中点，为半圆弧上的一点，且，，双曲线以为焦点且经过点.

（1）建立适当的平面直角坐标系，求双曲线方程；

（2）设过点的直线与双曲线相交于不同的两点，若的面积不小于，求直线的斜率的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 16 分

22．已知双曲线的左、右两个焦点为, ，动点P满足|P|+| P |=4。

（1）求动点P的轨迹E的方程；

（2）设过的直线交轨迹E于A、B两点，求以线段OA，OB 为邻边的平行四边形OAPB的顶点P的轨迹方程。

正确答案

（1）双曲线的方程可化为

∴P点的轨迹E是以为焦点，长轴为4的椭圆

由 ; 所求轨迹方程为

（2）略

解析

解析已在路上飞奔，马上就到！

知识点

直线与圆锥曲线的综合问题定义法求轨迹方程相关点法求轨迹方程

题型：单选题

单选题 · 5 分

11.若直线与双曲线（a>0，b>0）的交点在实轴上的射影恰好为双曲线的焦点，则双曲线的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

21.已知椭圆：（）的右焦点，右顶点,且．

（1）求椭圆的标准方程；

（2）若动直线：与椭圆有且只有一个交点，且与直线交于点,问：是否存在一个定点,使得.若存在，求出点坐标；若不存在，说明理由.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题圆锥曲线中的探索性问题

题型：单选题

单选题 · 4 分

18．点在直线上，若存在过的直线交抛物线于两点，且，则称点为“点”，那么下列结论中正确的是（）

A直线上的所有点都是“点”

B直线上仅有有限个点是“点”

C直线上的所有点都不是“点”

D直线上有无穷多个点（点不是所有的点）是“点”

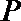
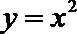
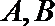
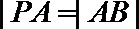
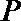
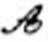
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两点间的距离公式抛物线的标准方程和几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

21．已知椭圆的中心在原点，焦点在y轴上，离心率为，且椭圆经过圆的圆心C。

（1）求椭圆的标准方程；

（2）设直线与椭圆交于A，B两点，点且|PA|=|PB|，求直线的方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程椭圆的定义及标准方程直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

20.如图，已知抛物线方程为。

（1）直线过抛物线的焦点F，且垂直于x轴，与抛物线交于A、B两点，求AB的长度。

（2）直线过抛物线的焦点，且倾斜角为，直线与抛物线相交于C、D两点，O为原点。求△OCD的面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 12 分

20．设椭圆的左、右焦点分别为F1、F2，下顶点为A，离心率，若直线l：过点A．

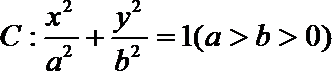
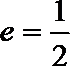
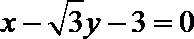
（I）求椭圆C的方程；

（II）在（I）的条件下，过右焦点F2作斜率为k的直线与椭圆C交于M、N两点，在x轴上是否存在点p(m，0)，使得以PM，PN为邻边的平行四边形是菱形，如果存在，求出m的取值范围；如果不存在，说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的探索性问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 直线与圆锥曲线的综合问题

扫码查看完整答案与解析