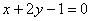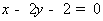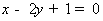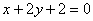- 轨迹方程的问题
- 共36题
1
题型:简答题
|
已知圆C:(x﹣4)2+(y﹣m)2=16(m∈N*),直线4x﹣3y﹣16=0过椭圆

(1)求m的值及椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求
正确答案
见解析。
解析
(1)因为直线4x﹣3y﹣16=0交圆C所得的弦长为
所以圆心C(4,m)到直线
即
又因为直线4x﹣3y﹣16=0过椭圆E的右焦点,所以右焦点坐标为F2(4,0)。
则左焦点F1的坐标为(﹣4,0),因为椭圆E过A点,
所以|AF1|+|AF2|=2a
所以
故椭圆E的方程为:
(2):
则
设x+3y=n,则由
消x得18y2﹣6ny+n2﹣18=0
由于直线x+3y=n与椭圆E有公共点,
所以△=(6n)2﹣4×18×(n2﹣18)≥0
所以﹣6≤n≤6,故
知识点
轨迹方程的问题
1
题型:简答题
|
如图,椭圆







(1)求椭圆
(2)若动点





正确答案
见解析。
解析
知识点
轨迹方程的问题
1
题型:
单选题
|
经过圆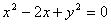
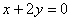
正确答案
A
解析
略
知识点
轨迹方程的问题
1
题型:简答题
|
如图,设








(1)若点


(2)设函数

正确答案
见解析
解析
(1)由题意,点



所以

所以
(2)由题意,
因为

所以


知识点
轨迹方程的问题
1
题型:填空题
|
13.有一个几何体的三视图及其尺寸如下(单位
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
轨迹方程的问题
下一知识点 : 二元二次方程表示圆的条件
扫码查看完整答案与解析