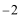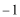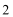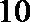- 函数的周期性
- 共47题
设函数
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当

正确答案
见解析。
解析
(1)
∴T=π,

故函数f(x)的单调递减区间是
(2)∵


当


知识点
已知f(x)=sin2x+sinxcosx,则f(x)的最小正周期和一个单调增区间分别为( )
正确答案
解析
f(x)=sin2x

所以函数的周期是:π;
由于


知识点
已知向量

(1)求函数
(2)在




正确答案
见解析
解析
(1)



=
所以函数

(2)
所以
因为C是三角形内角,所以



将


∴




知识点
16.给出下列三个命题:
①函数

②若函数





③若奇函数



正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
4.函数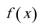
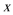
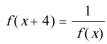
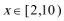
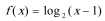
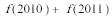
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=_______.
正确答案
-8
解析
解析已在路上飞奔,马上就到!
知识点
12.已知定义在R上的奇函数
①对任意x,都有
②当
则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设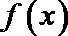
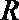
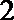
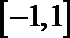
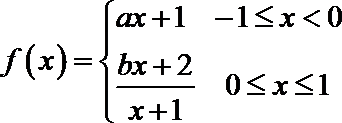
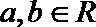

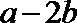
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在实数集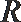
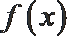
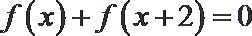
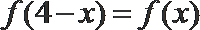
现有以下三种叙述:
①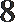
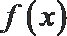
②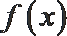
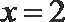
③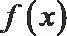
其中正确的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析