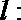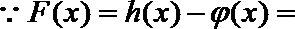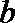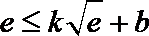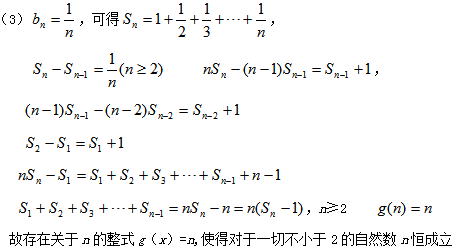- 函数恒成立、存在、无解问题
- 共23题
21.已知函数
(Ⅰ)求函数的定义域,并证明
(Ⅱ)对于

(Ⅲ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.若存在实常数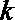
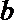
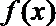
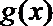
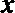
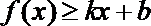
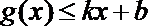
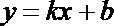
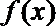
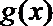
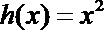
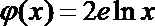
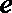
(1)求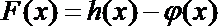
(2) 函数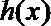
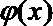
正确答案
(1) 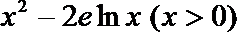
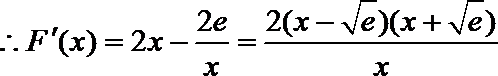

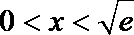
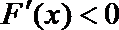
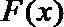
当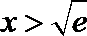
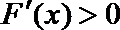
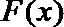
∴当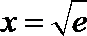
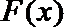
(2) 由(1)可知当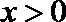
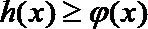

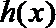
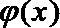
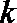

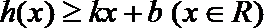
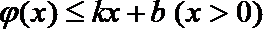
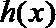
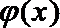

令
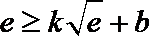
解析
解析已在路上飞奔,马上就到!
知识点
15.已知












①
②
③
④
则在区间

正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列



(1)求数列
(2)若函数

(3)设







正确答案
相加得:
所以
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,函数
若对



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(I)求函数
(II)已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列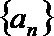
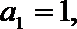
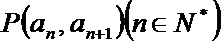
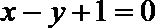
(1)求数列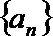
(2)若函数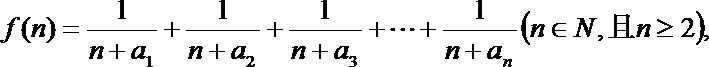
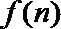
(3)设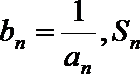
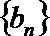
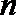
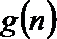
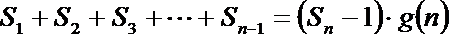
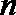
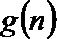
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 函数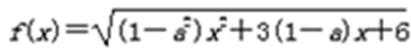
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析