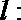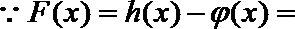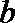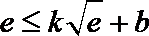- 函数恒成立、存在、无解问题
- 共23题
1
题型:简答题
|
21.已知函数
(Ⅰ)求函数的定义域,并证明
(Ⅱ)对于

(Ⅲ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
函数单调性的性质函数奇偶性的判断函数恒成立、存在、无解问题利用导数研究函数的单调性
1
题型:简答题
|
22.若存在实常数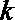
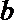
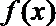
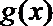
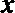
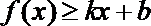
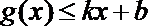
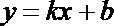
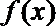
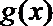
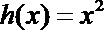
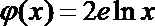
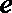
(1)求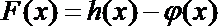
(2) 函数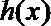
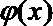
正确答案
(1) 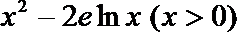
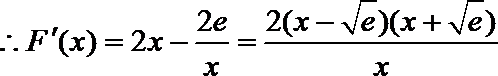

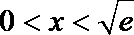
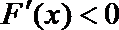
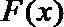
当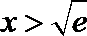
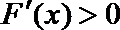
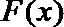
∴当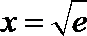
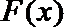
(2) 由(1)可知当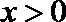
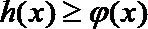

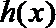
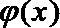
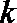

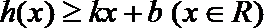
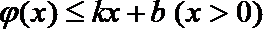
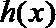
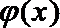

令
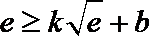
解析
解析已在路上飞奔,马上就到!
知识点
函数恒成立、存在、无解问题利用导数研究函数的单调性利用导数求函数的极值
1
题型:填空题
|
15.已知












①
②
③
④
则在区间

正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
函数的值域及其求法函数恒成立、存在、无解问题平面向量数量积的运算平面向量的综合题
1
题型:
单选题
|
16.不等式


正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
函数恒成立、存在、无解问题对数函数的图像与性质正弦函数的图象
1
题型:简答题
|
17. 函数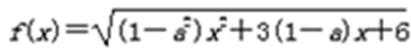
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
函数恒成立、存在、无解问题二次函数的图象和性质
已完结
扫码查看完整答案与解析