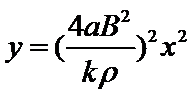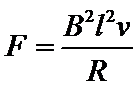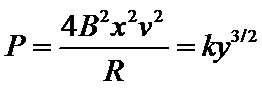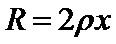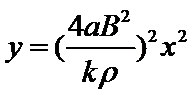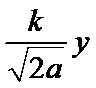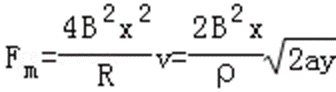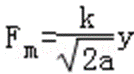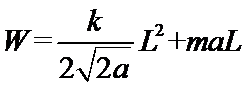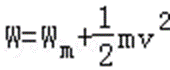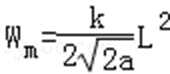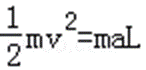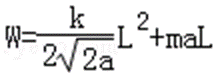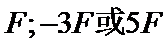- 通电直导线在磁场中受到的力
- 共166题
开学初,小源到建设银行营业网点兑换了此前在网上预约的中国高铁纪念币。这枚纪念币由中国人民银行发行,面额10元,每人限兑20枚,且需要提前预约。小源打算与班上同学分享自己的喜悦。他可以向大家这样介绍
①纪念币面额和实际购买力都是由中国人民银行规定的
②纪念币可以直接购买商品,也具有支付手段等货币职能
③纪念币发行量有限,具有一定的收藏价值和升值空间
④纪念币不能与同面额人民币等值流通,必须在规定时间地点使用
正确答案
解析
①错误,国家无权规定纪念币的实际购买力;④错误,纪念币与同面额人民币等值流通,在任何时间地点都可使用;由中国人民银行发行的纪念币属于法定货币,可以直接购买商品,也具有支付手段等货币职能,因其发行量有限,具有一定的收藏价值和升值空间,故②③正确。
知识点
如图,一关于y轴对称的导体轨道位于水平面内,磁感应强度为B的匀强磁场与平面垂直。一足够长,质量为m的直导体棒沿x轴方向置于轨道上,在外力F作用下从原点由静止开始沿y轴正方向做加速度为a的匀速加速直线运动,运动时棒与x轴始终平行。棒单位长度的电阻ρ,与电阻不计的轨道接触良好,运动中产生的热功率随棒位置的变化规律为P=ky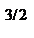
45.导体轨道的轨道方程y=f(x);
46.棒在运动过程中受到的安培力Fm随y的变化关系;
47.棒从y=0运动到y=L过程中外力F的功。
正确答案
解析
设棒运动到某一位置时与轨道接触点的坐标为(±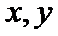
棒做匀加速运动
代入前式得
轨道形式为抛物线。
考查方向
闭合电路的欧姆定律.
解题思路
)求出安培力的功率及题给表达式,匀变速运动的速度位移关系,电阻关系式联立而得到轨道方程
易错点
功率公式以及电阻定律
正确答案
解析
安培力为:
以轨道方程代入得:
考查方向
解题思路
将安培力表示出来,联立轨道方程即可求解
易错点
安培力的表达式
正确答案
解析
由动能定理有:
安培力做功为:
棒在y=L处动能为:Ek=
外力做功为:
考查方向
解题思路
根据动能定理求外力做功
易错点
运用电磁感应的规律,如法拉第电磁感应定律、欧姆定律和安培力公式进行综合解题.
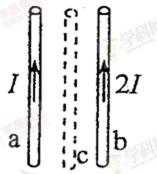
25.如图,两根通电长直导线a、b平行放置,a、b中的电流强度分别为I和2I,此时a受到的磁场力为F,若以该磁场力的方向为正,则b受到的磁场力为________。当在a、b的正中间再放置一根与a、b平行共面的通电长直导线c后,a受到的磁场力大小变为2F,则此时b受到的磁场力为________。
正确答案
25.−
解析
由安培定则和左手定则以及牛顿第三定律得b受到的磁场力为-F,由相互作用力原理得b受到的磁场力为-3F或5F
考查方向
解题思路
安培定则和左手定则分析b的磁场力
易错点
c的电流方向不确定
知识点
如图A.,两相距L=0.5m的平行金属导轨固定于水平面上,导轨左端与阻值R=2Ω的电阻连接,导轨间虚线右侧存在垂直导轨平面的匀强磁场。质量m=0.2kg的金属杆垂直置于导轨上,与导轨接触良好,导轨与金属杆的电阻可忽略。杆在水平向右的恒定拉力作用下由静止开始运动,并始终与导轨垂直,其v–t图像如图B.所示。在15s时撤去拉力,同时使磁场随时间变化,从而保持杆中电流为0。
求:
40.金属杆所受拉力的大小F;
41.0–15s内匀强磁场的磁感应强度大小B0;
42.15–20s内磁感应强度随时间的变化规律。
正确答案
由
由图可得
同理可知在15-20s时间段仅在摩擦力作用下运动。
右图由图可得
解得
解析
由
由图可得
同理计算F
考查方向
解题思路
分析图像由牛顿第二定律计算加速度,同理计算F
易错点
由图像获取信息的能力
正确答案
在10-15s时间段杆在磁场中做匀速运动,因此有
以

解得
解析
在10-15s时间段杆在磁场中做匀速运动,因此有

考查方向
解题思路
在10-15s时间段杆在磁场中做匀速运动,则受力平衡,有安培力的计算公式和受力平衡即可计算
易错点
方程的建立
正确答案
由题意可知在15-20s时间段通过回路的磁通量不变,设杆在10-15s内运动距离为

其中
由此可得
解析
15-20s时间段通过回路的磁通量不变,设杆在10-15s内运动距离为

考查方向
解题思路
磁通量不变是切入点,构建数学关系
易错点
方程的建立
25. 如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接。轨道宽度均为L=1m,电阻忽略不计。匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放。取g=10m/s2.
(1)求导体棒cd沿斜轨道下滑的最大速度的大小;
(2)若已知从开始运动到cd 棒达到最大速度的过程中,ab 棒产生的焦耳热Q=0.45J,求该过程中通过cd 棒横截面的电荷量;
(3)若已知cd 棒开始运动时距水平轨道高度h=10m,cd 棒由静止释放后,为使cd 棒中无感应电流,可让磁场Ⅱ的磁感应强度随时间变化,将cd 棒开始运动的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0=1T,试求cd 棒在倾斜轨道上下滑的这段时间内,磁场Ⅱ的磁感应强度B 随时间t 变化的关系式。
正确答案
(1)cd棒匀速运动时速度最大,设为vm,棒中感应电动势为E,电流为I,
感应电动势:E=BLvm,电流:I=
由平衡条件得:mgsinθ=BIL,代入数据解得:vm=1m/s;
(2)设cd从开始运动到达最大速度的过程中经过的时间为t,通过的距离为x,cd棒中平均感应电动势为E1,平均电流为I1,通过cd棒横截面的电荷量为q,
由能量守恒定律得:mgxsinθ=mvm2+2Q,
电动势:E1=

代入数据解得:q=1C;
(3)设cd棒开始运动时穿过回路的磁通量为Φ0,cd棒在倾斜轨道上下滑的过程中,设加速度大小为a,经过时间t通过的距离为x1,穿过回路的磁通量为Φ,cd棒在倾斜轨道上下滑时间为t0,则:Φ0=B0L
加速度:a=gsinθ,位移:x1=1/2(at2)
Φ=BL(

解得:t0=
为使cd棒中无感应电流,必须有:Φ0=Φ,
解得:B=

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析