- 角的变换、收缩变换
- 共13题
5.要得到函数

正确答案
解析
将函数





考查方向
解题思路
先将函数

易错点
三角函数相位变换公式不熟悉导致出错。
知识点
5.将函数


单位,得到的函数的图像的一个对称中心为()
正确答案
解析


考查方向
解题思路
该题是常规题1、平移得到新函数
易错点
本题易错在平移变化出错
知识点
已知函数f(x)=

(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
20.求f(x)的最小周期和最小值,
21.将函数f(x)的图像上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图像.当x
正确答案



解析
试题分析:(Ⅰ)首先用降幂公式将函数


试题解析: (1)

因此


考查方向
解题思路
本题考查三角恒等变形公式及正弦函数的图象及性质,第一问采用先降幂再用辅助角公式将已知函数化为
易错点
三角函数公式的正确运用;
正确答案

解析
试题分析:(Ⅱ)由题目所给变换及(Ⅰ)的化简结果求出函数

试题解析: (2)由条件可知:
当

从而

那么

故


考查方向
解题思路
本题考查三角恒等变形公式及正弦函数的图象及性质,第二小问在第一问的基础上应用三角函数图象变换知识首先求出函数
易错点
三角函数图象变换的性质规律;注意公式的准确性及变换时的符号
16.已知
(1)求
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知

正确答案
解析
略
知识点
已知

正确答案

解析
∵α,β∈(

∴



又sin(α+



∴cos(α+



∴sin(α﹣β)=﹣sin[(α+

=﹣[sin(α+



=﹣[



=
知识点
8.已知
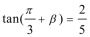

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(1)求
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量





(I)求
(II)求函数
(III)若

正确答案
(1)
(2)增区间[

(3)
解析
本题属于三角函数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求,
(2)对函数进行变形,转化成可用已知函数表示的形式,最后代入求值。
解:(I)f(x)=2



























考查方向
本题考查了向量的乘法、正(余)弦的二倍角、函数的单调区间、三角的恒等变形与化简求值等知识点,属于中档题,也是高考必考题型之一。向量的坐标式、向量的平行与垂直、三角函数的单调性、周期性、对称轴等知识常常会结合在一起进行命题。
易错点
1、二倍角的余弦公式中符号搞错
2、第(III)问的变形化简会出错
知识点
扫码查看完整答案与解析